题目内容
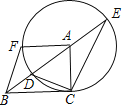
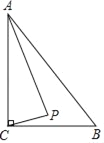
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=4,点P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段BP长的最小值是_____.
【答案】2.
【解析】
根据已知条件易证∠APC=90°,根据圆周角定理即可得点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,由此求得PB的长即可.
∵∠ACB=90°,
∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB
∴∠CAP+∠ACP=90°,
∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
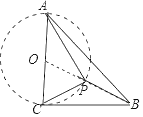
在Rt△CBO中,∵∠OCB=90°,BC=4,OC=3,
由勾股定理求得OB=5,
∴PB=OB﹣OP=5﹣3=2.
∴PB最小值为2.
故答案为:2.

练习册系列答案
相关题目