题目内容
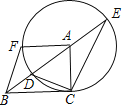
【题目】如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.
(1)求证:∠BCD=∠BEC;
(2)若BC=2,BD=1,求CE的长及sin∠ABF的值.
【答案】(1)见解析;(2)CE=![]() , sin∠ABF=
, sin∠ABF=![]() .
.
【解析】
(1)先利用等角的余角相等即可得出结论;
(2)先判断出△BDC∽△BCE得出比例式求出BE=4,DE=3,利用勾股定理求出CD,CE,再判断出△AFM∽△BAC,进而判断出四边形FNCA是矩形,求出FN,NC,即:BN,再用勾股定理求出BF,即可得出结论.
(1)∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵DE是⊙A的直径,
∴∠DCE=90°,
∴∠BEC+∠CDE=90°,
∵AD=AC,
∴∠CDE=∠ACD,
∴∠BCD=∠BEC,
(2)∵∠BCD=∠BEC,∠EBC=∠EBC,
∴△BDC∽△BCE,
∴![]() ,
,
∵BC=2,BD=1,
∴BE=4,EC=2CD,
∴DE=BE﹣BD=3,
在Rt△DCE中,DE2=CD2+CE2=9,
∴CD=![]() ,CE=
,CE=![]() ,
,
过点F作FM⊥AB于M,
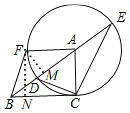
∵∠FAB=∠ABC,∠FMA=∠ACB=90°,
∴△AFM∽△BAC,
∴![]() ,
,
∵DE=3,
∴AD=AF=AC=![]() ,AB=
,AB=![]() ,
,
∴FM=![]() ,
,
过点F作FN⊥BC于N,
∴∠FNC=90°,
∵∠FAB=∠ABC,
∴FA∥BC,
∴∠FAC=∠ACB=90°,
∴四边形FNCA是矩形,
∴FN=AC=![]() ,NC=AF=
,NC=AF=![]() ,
,
∴BN=![]() ,
,
在Rt△FBN中,BF=![]() ,
,
在Rt△FBM中,sin∠ABF=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() ℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() ℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() ℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录
℃时,制冷再次停止,…,按照以上方式循环进行.同学们记录![]() 内9个时间点冷柜中的温度
内9个时间点冷柜中的温度![]() (℃)随时间
(℃)随时间![]() 变化情况,制成下表:
变化情况,制成下表:
时间 | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | … |
温度 | … |
|
|
|
|
|
|
|
|
| … |
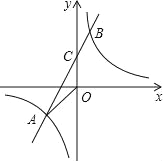
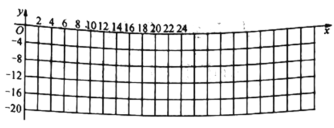
(1)如图,在直角坐标系中,描出上表数据对应的点,并画出当![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象;
变化的函数图象;
(2)通过图表分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
②当![]() 时,写出符合表中数据的函数解析式;
时,写出符合表中数据的函数解析式;
(3)当前冷柜的温度![]() ℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?
℃时,冷柜继续工作36分钟,此时冷柜中的温度是多少?