Question

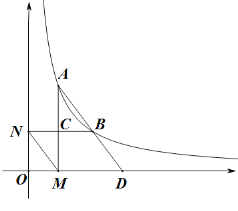
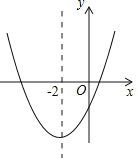
【题目】如图，在平面直角坐标系xOy中，反比例函数y＝﹣在第二象限的图象上有一点A，过点A作AB⊥x轴于点B，则S△AOB＝_____．

Answer 1

【答案】2

【解析】

设出A的坐标为（a，b），根据A为第二象限的点，得到a小于0，b大于0，进而表示出AB及OB的长，再由A为反比例函数图象上，将A坐标代入反比例函数解析式中，得到-ab=4，最后由三角形AOB为直角三角形，利用两直角边乘积的一半表示出三角形AOB的面积，将-ab=4代入，即可求出三角形AOB的面积．

解：设A的坐标为（a，b）（a＜0，b＞0），
则OB=-a，AB=b，
又∵A在反比例函数y=-图象上，
∴将x=a，y=b代入反比例函数解析式得：b=- ，即-ab=4，
又∵△AOB为直角三角形，
∴S△AOB=OBAB=-ab=2．
故答案为：2．