��Ŀ����
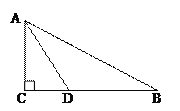
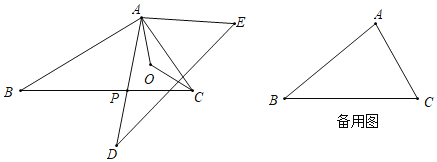
����Ŀ����ͼ���ڡ�ABC�͡�ADE�У���P���߶�BC�ϵĶ��㣨P����B��C�غϣ�����AD����P�㣻��֪��B����D��30�㣬BC��DE��AB��AD��10����PAC��ƽ�������ACB��ƽ���߽���O��
��1����BAD���CAE�����˵�������ɣ�
��2����AP��Ϊm�����ú�m�Ĵ���ʽ��ʾ�߶�PD�ij�������PD�����ֵ��
��3������BAC��90��ʱ�����㣼��AOC�����㣬��ô������ ���������� ����
���𰸡���1����BAD����CAE������������2��PD��10��m��5����3��105,150
��������
��1��������SAS֤����ABC�ա�ADE��Ȼ��ó���BAC����DAE��ͨ�������������ɵó���BAD����CAE��
��2��PD��AD��AP��10��m���ɵ�P���߶�BC���Ҳ���B��C�غϣ��ó�AP����Сֵ��AP��BCʱAP�ij��ȣ���ʱPD�ɵ����ֵ��
��3��OΪ��APC��ƽ���ߵĽ��㣬Ӧ�á��������ڽǺ͵���180�㡰����ƽ���߶��弴�ɱ�ʾ����AOC���Ӷ��õ���������ֵ��
�⣺��1����BAD����CAE���������£�
��ͼ��ʾ��
�ڡ�ABC�͡�ADE�У�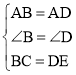 ��
��
���ABC�ա�ADE��SAS��
���BAC����DAE
����BAD+��DAC����DAC+��CAE
���BAD����CAE��
��2����AD��10��AP��m��
��PD��10��m
��AD��BCʱ��AP��С����PD���
![]()
��AP��![]() AB��5��
AB��5��
��PD��10��5��5
��PD�����ֵΪ5��
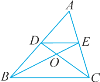
��3����ͼ2�����BAP��![]() �����APC��
�����APC��![]() ��
��
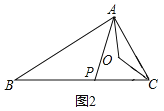
��AB��AC��![]() ��
��
���BAC��90�㣬��PCA��60�㣬��PAC��![]() ��
��
�ߡ�PAC��ƽ�������ACB��ƽ���߽���O��
���OAC��![]() ��PAC����OCA��
��PAC����OCA��![]() ��PCA
��PCA
��![]()
![]()
![]()
![]()
![]()
![]()
��![]()
������105������150��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�