题目内容
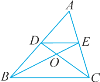
【题目】 如图，在平行四边形ABCD中，∠C=60°，M、N分别是AD、BC的中点，BC=2CD．
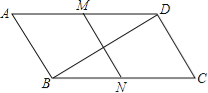
（1）求证：四边形MNCD是平行四边形；
（2）求证：BD=
MN．
【答案】见解析
【解析】
试题（1）根据平行四边形的性质，可得AD与BC的关系，根据MD与NC的关系，可得证明结论；
（2）根据根据等边三角形的判定与性质，可得∠DNC的度数，根据三角形外角的性质，可得∠DBC的度数，根据正切函数，可得答案．
证明：（1）∵ABCD是平行四边形，
∴AD=BC，AD∥BC，
∵M、N分别是AD、BC的中点，
∴MD=NC，MD∥NC，
∴MNCD是平行四边形；
（2）如图：连接ND，
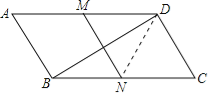
∵MNCD是平行四边形，
∴MN=DC．
∵N是BC的中点，
∴BN=CN，
∵BC=2CD，∠C=60°，
∴△NCD是等边三角形．
∴ND=NC，∠DNC=60°．
∵∠DNC是△BND的外角，
∴∠NBD+∠NDB=∠DNC，
∵DN=NC=NB，
∴∠DBN=∠BDN=
∠DNC=30°，
∴∠BDC=90°．
∵tan
，
∴DB=
DC=MN．
练习册系列答案
相关题目
【题目】某校积极开展“我爱我的祖国”教育知识竞赛，八年级甲、乙两班分别选5名同学参加比赛，其预赛成绩如图所示：
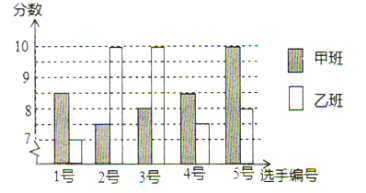
（1）根据上图填写下表：
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
（2）根据上表数据，分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析．
