题目内容
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.

【答案】(2,5)
【解析】
将一次函数与二次函数组成方程组,得到关于x的一元二次方程,利用根与系数的关系建立起
系数与根的关系,又知两直线垂直,可得斜率之积为-1,列出关于x、y的方程,利用根与系数的关系将方程转化为直线的解析式,再判断其所过定点.
设A(x1,y1),B(x2,y2),直线AB的解析式为y=kx+b
由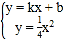 得
得![]()
∴x1+x2=4k,x1x2=-4b,
y1+y2=![]() =4
=4![]()
y1y2=![]()
∵AD⊥BD
kAD·kBD=-1
![]()
∴(y1-1)(y2-1)+( x1+2)(x2+2)=0
代入得
![]() ,
,
![]()
![]() 或b=-2k+5
或b=-2k+5
代入y=kx+b
得y=kx+ 2k+1=k(x+2)+1,或y= kx-2k+5=k(x-2) +5
显然AB不过(-2,1)点
所以直线AB的解析式为y=(x-2)k+5,AB过定点(2,5)

练习册系列答案
相关题目