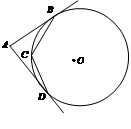题目内容
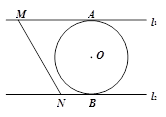
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是( )

| A.l1和l2的距离为2 |
B.当MN与⊙O相切时,AM=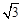 |
C.MN=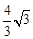 |
| D.当∠MON=90°时,MN与⊙O相切 |
B.
试题分析:如图2,连结OA、OB,根据切线的性质和l1∥l2得到AB为⊙O的直径,则l1和l2的距离为2;当MN与⊙O相切,连结OM,ON,当MN在AB左侧时,根据切线长定理得∠AMO=∠AMN=30°,在Rt△AMO中,利用正切的定义可计算出AM=
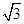 ,在Rt△OBN中,由于∠ONB=∠BNM=60°,可计算出BN=
,在Rt△OBN中,由于∠ONB=∠BNM=60°,可计算出BN=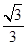 ,当MN在AB右侧时,AM=
,当MN在AB右侧时,AM=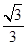 ,所以AM的长为
,所以AM的长为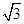 或
或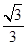 ;当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,易证得Rt△OAF≌Rt△OBN,则OF=ON,于是可判断MO垂直平分NF,所以OM平分∠NOF,根据角平分线的性质得OE=OA,然后根据切线的判定定理得到MN为⊙O的切线.
;当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,易证得Rt△OAF≌Rt△OBN,则OF=ON,于是可判断MO垂直平分NF,所以OM平分∠NOF,根据角平分线的性质得OE=OA,然后根据切线的判定定理得到MN为⊙O的切线.故选B.

练习册系列答案
相关题目
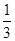 圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为__________.
圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为__________.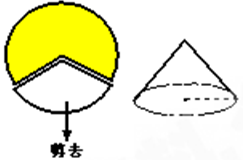

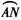 的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .
的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .