题目内容
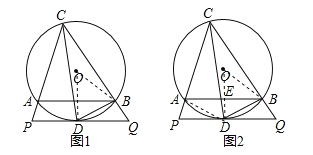
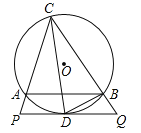
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;
(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;
(3)根据题意得到ACBQ=4,得到BD=2,由(1)知PQ是⊙O的切线,由切线的性质得到OD⊥PQ,根据平行线的性质得到OD⊥AB,根据三角函数的定义得到BE=3DE,根据勾股定理得到BE的长,设OB=OD=R,根据勾股定理即可得到结论.
试题解析:(1)证明:∵PQ∥AB,∴∠ABD=∠BDQ=∠ACD,∵∠ACD=∠BCD,∴∠BDQ=∠ACD,如图1,连接OB,OD,交AB于E,则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,在△OBD中,∠OBD+∠ODB+∠O=180°,∴2∠ODB+2∠O=180°,∴∠ODB+∠O=90°,∴PQ是⊙O的切线;
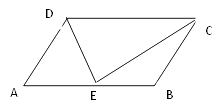
(2)证明:如图2,连接AD,由(1)知PQ是⊙O的切线,∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,∴AD=BD,∵∠DBQ=∠ACD,∴△BDQ∽△ACD,∴![]() ,∴BD2=ACBQ;
,∴BD2=ACBQ;
(3)解:方程![]() 可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程
可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程![]() 的两实根,∴ACBQ=4,由(2)得BD2=ACBQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=
的两实根,∴ACBQ=4,由(2)得BD2=ACBQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=![]() ,∴tan∠ABD=
,∴tan∠ABD=![]() ,∴BE=3DE,∴DE2+(3DE)2=BD2=4,∴DE=
,∴BE=3DE,∴DE2+(3DE)2=BD2=4,∴DE=![]() ,∴BE=
,∴BE=![]() ,设OB=OD=R,∴OE=R﹣
,设OB=OD=R,∴OE=R﹣![]() ,∵OB2=OE2+BE2,∴R2=(R﹣
,∵OB2=OE2+BE2,∴R2=(R﹣![]() )2+(
)2+(![]() )2,解得:R=
)2,解得:R=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.