题目内容
【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )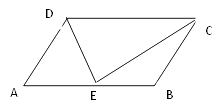
A.96
B.48
C.60
D.30
【答案】B
【解析】解:∵AB∥CD,
∴∠CDE=∠AED.
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AE=AD=5.
同理可得:BE=BC=5,
∴AB=5+5=10,
∴CD=10.
∵DE平分∠ADC,CE平分∠BCD,
∴∠CDE+∠DCE=90°,
∴∠CED=90°.
由勾股定理得
![]() .
.
![]() ,
,
![]() .
.
故选B.
【考点精析】本题主要考查了平行线的性质和三角形的面积的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的面积=1/2×底×高才能正确解答此题.

练习册系列答案
相关题目