题目内容
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
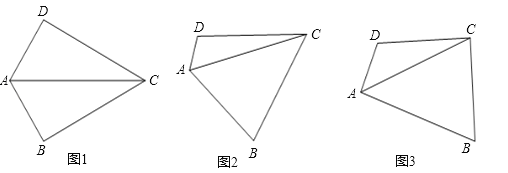
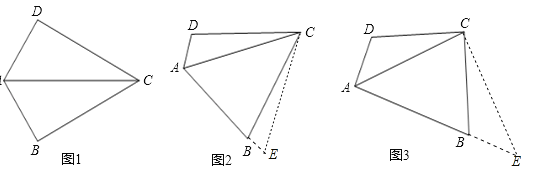
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
【答案】(1)AC=AD+AB;(2)成立;(3)AD+AB=![]() AC.
AC.
【解析】
试题分析:(1)结论:AC=AD+AB,只要证明AD=![]() AC,AB=
AC,AB=![]() AC即可解决问题;
AC即可解决问题;
(2)(1)中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;
(3)结论:AD+AB=![]() AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
试题解析:(1)AC=AD+AB.
理由如下:如图1中,在四边形ABCD中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC平分∠DAB,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=![]() AC,同理AD=
AC,同理AD=![]() AC,∴AC=AD+AB.
AC,∴AC=AD+AB.
(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,如图2,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠B=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CB,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.
(3)结论:AD+AB=![]() AC.理由如下:
AC.理由如下:
过点C作CE⊥AC交AB的延长线于点E,如图3,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°,∴AC=CE.
又∵∠D+∠B=180°,∠D=∠CBE,∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.
在Rt△ACE中,∠CAB=45°,∴AE=![]() =
=![]() AC,∴AD+AB=
AC,∴AD+AB=![]() AC.
AC.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案