Question

【题目】如图，在△ABC中，AB＝AC，D、E、F分别为AB、BC、AC的中点，则下列结论：①△ADF≌△FEC；②四边形ADEF为菱形；③。其中正确的结论是____________.（填写所有正确结论的序号）

Answer 1

【答案】①②③

【解析】

①根据三角形的中位线定理可得出AD=FE、AF=FC、DF=EC，进而可证出△ADF≌△FEC（SSS），结论①正确；

②根据三角形中位线定理可得出EF∥AB、EF=AD，进而可证出四边形ADEF为平行四边形，由AB=AC结合D、F分别为AB、AC的中点可得出AD=AF，进而可得出四边形ADEF为菱形，结论②正确；

③根据三角形中位线定理可得出DF∥BC、DF=BC，进而可得出△ADF∽△ABC，再利用相似三角形的性质可得出，结论③正确．此题得解．

①∵D、E、F分别为AB、BC、AC的中点，

∴DE、DF、EF为△ABC的中位线，

∴AD=AB=FE，AF=AC=FC，DF=BC=EC．

在△ADF和△FEC中，

，

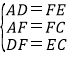∴△ADF≌△FEC（SSS），结论①正确；

②∵E、F分别为BC、AC的中点，

∴EF为△ABC的中位线，

∴EF∥AB，EF=AB=AD，

∴四边形ADEF为平行四边形．

∵AB=AC，D、F分别为AB、AC的中点，

∴AD=AF，

∴四边形ADEF为菱形，结论②正确；

③∵D、F分别为AB、AC的中点，

∴DF为△ABC的中位线，

∴DF∥BC，DF=BC，

∴△ADF∽△ABC，

∴，结论③正确．

故答案为：①②③．