题目内容
【题目】如图,在菱形ABCD中,AB=5cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB.CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由题意知道AE=t,CF=2t,连接BD,证明△DEB≌△DFC,得到EB=FC=2t,进而AB=AE+EB=3t=5,进而求出t的值.
解:连接DB,如下图所示,
∵四边形ABCD为菱形,且∠ADC=120°,
∴∠CDB=60°
∴△CDB为等边三角形,∴DB=DC
又∵△DEF为等边三角形,∴∠EDF=60°,DE=DF
∴∠CDB=∠EDF
∴∠CDB-∠BDF=∠EDF-∠BDF
∴∠CDF=∠BDE
在△EDB和△FDC中:
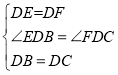 ,∴△EDB≌△FDC(SAS)
,∴△EDB≌△FDC(SAS)
∴FC=BE=2t
∴AB=AE+EB=t+2t=3t=5
∴t=![]() .
.
故答案为:D.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目