题目内容
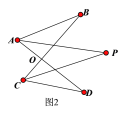
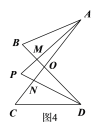
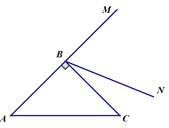
【题目】如图,BN是等腰Rt△ABC的外角∠CBM内部的一条射线,∠ABC=90°,AB=CB,点C关于BN的对称点为D,连接AD,BD,CD,其中CD,AD分别交射线BN于点E,P.
(1)依题意补全图形;
(2)若∠CBN=![]() ,求∠BDA的大小(用含
,求∠BDA的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段PB,PA与PE之间的数量关系,并证明.
【答案】(1)补图见解析;(2)45°-![]() ;(3)PA=
;(3)PA=![]() (PB+PE)..
(PB+PE)..
【解析】
此题涉及的知识点是对称点的画法,角大小的求解,数量关系的证明,解答时第一问根据已知条件直接画图,连线;第二问根据对称图形性质可以算出角的大小;第三问证明两三角形全等就可以得到线段之间的关系。
解:(1) 如图所示:
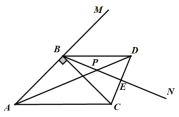
(2)∵∠ABC=90°
∴∠MBC=∠ABC=90°
∵点C关于BN的对称点为D
∴BC=BD,∠CBN=∠DBN=![]()
∵AB=BC
∴AB=BD
∴∠BAD=∠ADB=![]() =45°-
=45°-![]()
(3)猜想:![]()
证明:
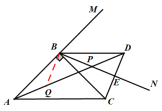
过点B作BQ⊥BE交AD于Q
∵∠BPA=∠DBN+∠ADB,∠ADB=45°-![]() ,∠DBN=
,∠DBN=![]()
∴∠BPA=∠DPE=45°
∵点C关于BN的对称点为D
∴BE⊥CD
∴PD=![]() PE,PQ=
PE,PQ=![]() PB,
PB,
∵BQ⊥BE,∠BPA=45°
∴∠BPA=∠BQP=45°
∴∠AQB=∠DPB=135°
又∵AB=BD,∠BAD=∠ADB
∴△AQB≌△BPD(AAS)
∴AQ=PD
∵PA=AQ+PQ
∴![]()

练习册系列答案
相关题目