题目内容
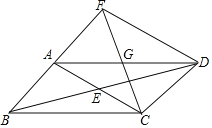
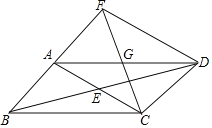
【题目】如图,![]() 的对角线
的对角线![]() 与
与![]() 相交于点E,点G为
相交于点E,点G为![]() 的中点,连接
的中点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点F,连接
的延长线于点F,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断四边形
,判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
【答案】(1)证明见解析;(2)矩形,证明见解析
【解析】
(1)根据ASA定理证得△AGF≌△DGC,从而得到GF=GC,求得四边形ACDF是平行四边形,然后根据平行四边形的性质求证![]()
![]() ;
;
(2)利用平行四边形的判定与性质结合全等三角形的性质得出△AFG是等边三角形,从而得到AD=CF,再利用矩形的判定方法得出答案.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FAG=∠CDG,
∵点G是AD的中点,
∴GA=GD,
在△AGF和△DGC中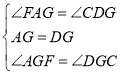 ,
,
∴△AGF≌△DGC(ASA);
∴GF=GC,AF=DC
∴四边形ACDF是平行四边形
∴AC=DF
又∵在平行四边形ABCD中,![]()
∴![]() ;
;
(2)解:四边形ACDF是矩形.
理由:由(1)可知四边形是ACDF平行四边形,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=AF,
又∵AG=AB,
∴AG=AF,
∴AB=AG=AF,
∵四边形ABCD是平行四边形,AD∥BC,∠BCD=120°
∴∠BAD=120°,∠FAG=60°,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,
∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】为了调查学生对数学知识的理解和应用,某校学生会专门针对七年级举办了“数学知识应用创新能力”测试,七年级的所有学生都参加了测试,试卷共有![]() 道题,每题
道题,每题![]() 分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
组别 | 成绩 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
合计 |
|

(![]() )频数分布表中
)频数分布表中![]() 的值等于 ;
的值等于 ;
(![]() )请把频数分布直方图补充完整;
)请把频数分布直方图补充完整;
(![]() )若测试成绩不低于
)若测试成绩不低于![]() 分为优秀,请你估计七年级
分为优秀,请你估计七年级![]() 名学生成绩优秀的有多少人?
名学生成绩优秀的有多少人?