题目内容
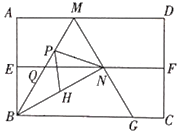
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
【答案】①④⑤
【解析】如图1,连接AN,
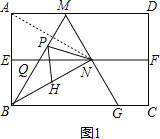
∵EF垂直平分AB,
∴AN=BN,
根据折叠的性质,可得
AB=BN,
∴AN=AB=BN.
∴△ABN为等边三角形。
∴∠ABN=60°,∠PBN=60°÷2=30°,
即结论①正确;
∵∠ABN=60°,∠ABM=∠NBM,
∴∠ABM=∠NBM=60°÷2=30°,
∴AM=ABtan30°=2×![]() =
=![]() ,
,
即结论②不正确。
∵EF∥BC,QN是△MBG的中位线,
∴QN=![]() BG;
BG;
∵BG=BM=AB÷cos∠ABM=2÷![]() =
=![]() ,
,
∴QN=![]() ×
×![]() =
=![]() ,
,
即结论③不正确。
∵∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,
∴∠BMG=∠BNM∠MBN=90°30°=60°,
∴∠MBG=∠ABG∠ABM=90°30°=60°,
∴∠BGM=180°60°-60°=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,
即结论④正确。
∵△BMG是等边三角形,点N是MG的中点,
∴BN⊥MG,∴BN=BGsin60°=![]() ×
×![]() =2,
=2,
根据条件易知E点和H点关于BM对称,
∴PH=PE,
∴P与Q重合时,PN+PH的值最小,此时PN+PH=PN+PE=EN,
∵EN=![]() =
=![]() ,
,
∴PN+PH=![]() ,
,
∴PN+PH的最小值是![]() ,
,
即结论⑤正确。
故答案为:①④⑤。

练习册系列答案
相关题目