题目内容
【题目】已知关于x的一元二次方程mx2+2mx+m﹣4=0;
(1)若该方程没有实数根,求m的取值范围.
(2)怎样平移函数y=mx2+2mx+m﹣4的图象,可以得到函数y=mx2的图象?
【答案】(1)m<0;(2)向右平移1个单位长度,再向上平移4个单位长度.
【解析】
(1)根据关于x的一元二次方程mx2+2mx+m﹣4=0没有实数根,可以得到关于m的不等式组,从而可以求得m的取值范围;
(2)先将函数y=mx2+2mx+m﹣4化为顶点式,再根据平移的性质可以得到函数y=mx2.
(1)∵关于x的一元二次方程mx2+2mx+m﹣4=0没有实数根,
∴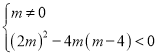 ,
,
解得,m<0,
即m的取值范围是m<0;
(2)∵函数y=mx2+2mx+m﹣4=m(x+1)2﹣4,
∴函数y=mx2+2mx+m﹣4的图象向右平移一个单位长度,在向上平移4个单位长度即可得到函数y=mx2的图象.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目