Question

【题目】如图，直线分别交轴于A、C，点P是该直线与反比例函数在第一象限内的一个交点，PB⊥轴于B，且S△ABP=9．

（1）求证：△AOC∽△ABP；

（2）求点P的坐标；

（3）设点R与点P在同一个反比例函数的图象上，且点R在直线PB的右侧，作RT⊥轴于T，当△BRT与△AOC相似时，求点R的坐标．

Answer 1

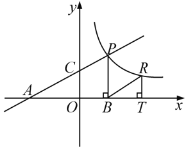
【答案】（1）详见解析；（2）P为（2，3）；（3）R（）或（3，0）

【解析】

（1）由一对公共角相等，一对直角相等，利用两对角相等的三角形相似即可得证；
（2）先求出点A、C的坐标，设出A（x，0），C（0，y）代入直线的解析式可知；由△AOC∽△ABP，利用线段比求出BP，AB的值从而可求出点P的坐标即可；
（3）把P坐标代入求出反比例函数，设R点坐标为（），根据△BRT与△AOC相似分两种情况，利用线段比建立方程，求出a的值，即可确定出R坐标．

解：（1）∵∠CAO=∠PAB，∠AOC=∠ABP=90°，

∴△AOC∽△ABP；

（2）设A（x，0），C（0，y）由题意得：

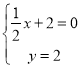，解得：，
∴A（-4，0），C（0，2），即AO=4，OC=2，
又∵S△ABP=9，
∴ABBP=18，
又∵PB⊥x轴，
∴OC∥PB，
∴△AOC∽△ABP，
∴，即，
∴2BP=AB，
∴2BP2=18，
∴BP2=9，
∴BP=3，
∴AB=6，
∴P点坐标为（2，3）；

（3）设反比例函数为，则，即，

可设R点为（），则RT=，TB=

①要△BRT∽△ACO，则只要，

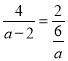∴，解得：，

∴；

∴点R的坐标为：（，）；

②若△BRT∽△CAO，则只要，

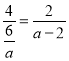∴，解得：，

∴，

∴点R的坐标为：（3，2）；

综合上述可知，点R为：（）或（3，2）.