题目内容
【题目】如图，是反比例函数
与
在x轴上方的图象，点C是y轴正半轴上的一点，过点C作
轴分别交这两个图象与点A和点B，P和Q在x轴上，且四边形ABPQ为平行四边形，则四边形ABPQ的面积等于（ ）
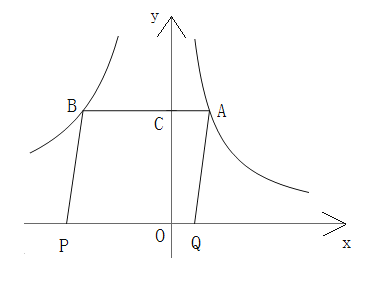
A.20B.15C.10D.5
【答案】C
【解析】
分别过A、B作AD、BE垂直x轴，易证
，则平行四边形ABPQ的面积等于矩形ADEB的面积，根据反比例函数比例系数k的几何意义分别求得矩形ADOC和矩形BEOC的面积，相加即可求得结果．
解：如图，分别过A、B作AD、BE垂直x轴于点D、点E，则四边形ADEB是矩形，
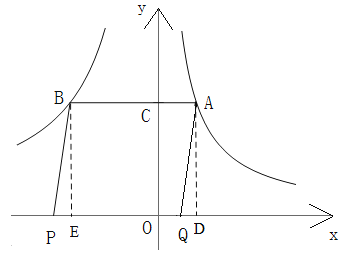
易证，
∴
S矩形ABED，
∵点A在反比例函数
上，
由反比例函数比例系数k的几何意义可得：
S矩形ADOC=|k|=3，
同理可得：S矩形BEOC=7，
∴S矩形ABED= S矩形ADOC+S矩形BEOC=3+7=10，
故选：C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
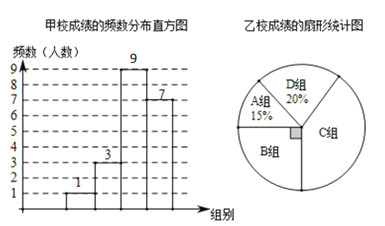
【题目】为了解甲、乙两校学生英语口语的学习情况，每个学校随机抽取
个学生进行测试，测试后对学生的成绩进行了整理和分析，绘制成了如下两幅统计图，（数据分组为：
组：
，
组：
，
组：
，
组：
）
a．甲校学生的测试成绩在组的是：
，
，，，
，，
，
，
b．甲、乙两校成绩的平均数，中位数，众数如表：
平均数 | 中位数 | 众数 | |
甲校 | 83.2 | a | 82.5 |
乙校 | 80.6 | 81 | 80 |
根据以上信息，回答下列问题：
（1）扇形统计图中组所在的圆心角度数为____度，乙校学生的测试成绩位于组的人数为___人
（2）表格中
_________在此次测试中，甲校小明和乙校小华的成绩均为分，则两位同学在本校测试成绩中的排名更靠前的是________（填小明或小华）．
（3）假设甲校学生共有
人参加此次测试，估计成绩超过
分的人数．
