题目内容
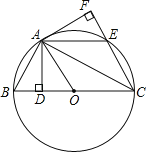
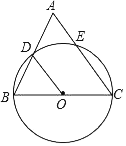
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为⊙O的切线;
(2)设BE与⊙O交于点F,AF的延长线与EC交于点P,已知∠PCF=∠CBF,PC=5,PF=3.求:cos∠PEF的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而得到CE是圆O的切线.
(2)利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PEA、△PCF∽△PAC,从而得到PC=PE=5.然后求出cos∠PEF的值.
(1)证明:∵CE⊥AD于点E
∴∠DEC=90°,
∵BC=CD,
∴C是BD的中点,
又∵O是AB的中点,
∴OC是△BDA的中位线,
∴OC∥AD,
∴∠OCE=∠CED=90°,
∴OC⊥CE,
又∵点C在圆上,
∴CE是圆O的切线;
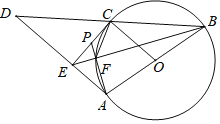
(2)连接AC,
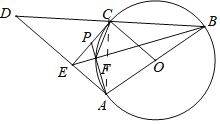
∵AB是直径,点F在圆上
∴∠AFB=∠PFE=90°=∠CEA,
∵∠EPF=∠EPA,
∴△PEF∽△PEA,
∴PE2=PF×PA,
∵∠FBC=∠PCF=∠CAF,
又∵∠CPF=∠CPA,
∴△PCF∽△PAC,
∴PC2=PF×PA,
∴PE=PC,
在直角△PEF中,
∴EF=4,cos∠PEF=![]() .
.

练习册系列答案
相关题目