题目内容
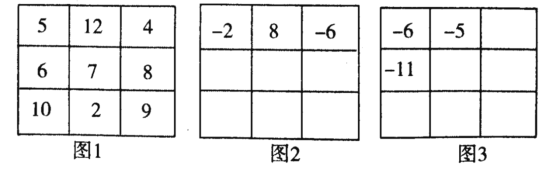
【题目】将九个数填在3×3（3行3列）的方格中，如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等，这样的图称为“广义的三阶幻方”，如图1就是一个满足条件的广义三阶幻方.图2、图3的广义三阶幻方中分别给出了三个数.请直接将图2、图3的其余6个数全填上；
（提示：三阶幻方的幻和=中心数字×3）
【答案】见解析
【解析】
根据图中的数据先求出三阶幻方的幻和=
，然后利用三阶幻方的幻和=中心数字×3求出中心数，接下来进一步利用三阶幻方的幻和为0求取所剩的每一个数即可；在图3中，先设其余六个数分别为A、B、C、D、E、X，然后根据广义的三阶幻方，两粗线的6个数之和等于两细线的6个数之和，据此建立方程然后进一步变形求解即可.
如图2所示，三阶幻方的幻和=，
又∵三阶幻方的幻和=中心数字×3，
∴在图2中的中心数字为0，
∴对角线右下角数字为：
；
对角线左下角数字为：
；
中心数下方数字为;
;
中心数左边数字为：
；
中心数右边数字为：
；
∴图2具体填表如下：
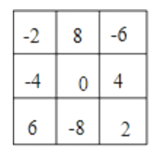
如图，设图3中各数为A、B、C、D、E、X，
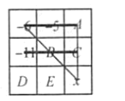
① 根据广义的三阶幻方，两粗线的6个数之和等于两细线的6个数之和，
∴
，
∴
，
∴
，
② ∵三阶幻方的幻和=中心数字×3，
∴
，
∴
，
③ ∵三阶幻方的幻和=中心数字×3，
∴
，
∴
，
同理可得：
，
，
，
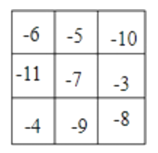
∴图3具体填表如下：
练习册系列答案
相关题目
