题目内容
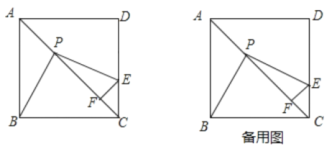
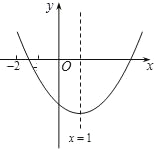
【题目】如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.
(1)依题意补全图形;
(2)求∠AGE的度数(用含α的式子表示);
(3)用等式表示线段EG与EF,AF之间的数量关系,并说明理由.

【答案】(1)见解析;(2)60°-α;(3)见解析
【解析】试题分析:![]() 根据题意补全图形即可.
根据题意补全图形即可.
![]() 根据轴对称的性质得:AE=AG=AD. ∠EAC=∠BAC+∠BAE=30°+α,
根据轴对称的性质得:AE=AG=AD. ∠EAC=∠BAC+∠BAE=30°+α,
∠EAG=2∠EAC=60°+2α,根据等腰三角形的性质,即可求出∠AGE的度数.
![]() 设AC交EG于点H根据∠BAC=30°,∠AHF=90°,得到
设AC交EG于点H根据∠BAC=30°,∠AHF=90°,得到![]()
![]() 又因点E,G关于AC对称EG=2EH
又因点E,G关于AC对称EG=2EH
![]()
试题解析:![]()
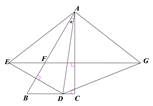
(2)由轴对称性可知,AB为ED的垂直平分线,AC为EG的垂直平分线.
∴AE=AG=AD.
∴∠AEG=∠AGE,∠BAE=∠BAD=α,
∴∠EAC=∠BAC+∠BAE=30°+α,
∴∠EAG=2∠EAC=60°+2α,
∴![]()
或:∠AGE=∠AEG=90°-∠EAC=90°-(∠BAC+∠EAB)=90°-(30°+α)=60°-α,
(3)EG=2EF+AF,
法1:设AC交EG于点H,
∵∠BAC=30°,∠AHF=90°,
∴![]()
![]()
又∵点E,G关于AC对称,
∴EG=2EH,
∴![]()
法2:在FG上截取NG=EF,连接AN.
又∵AE=AG,
∴∠AEG=∠AGE,
∴△AEF≌△AGN,
∴AF=AN,
∵∠EAF=α,∠AEG=60°-α,
∴∠AFN=60°,
∴△AFN为等边三角形,
∴AF=FN,
∴EG=EF+FN+NG=2EF+AF.

练习册系列答案
相关题目