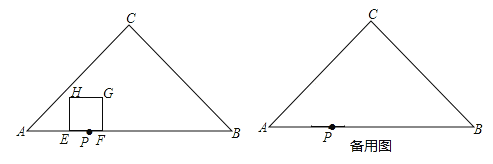题目内容
【题目】如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=![]() AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8![]() ,其中正确的结论是______(只填序号).
,其中正确的结论是______(只填序号).

【答案】①②③.
【解析】解:∵AE=![]() AB=2,∴AB=3×2=6,BE=6﹣2=4.∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴BE=PE=4,即AE=
AB=2,∴AB=3×2=6,BE=6﹣2=4.∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴BE=PE=4,即AE=![]() BE=
BE=![]() PE.∵四边形ABCD是矩形,∴∠ABC=90°,∠A=90°,∴∠APE=30°,∴∠AEP=60°.∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴∠BEF=∠FPE=
PE.∵四边形ABCD是矩形,∴∠ABC=90°,∠A=90°,∴∠APE=30°,∴∠AEP=60°.∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴∠BEF=∠FPE=![]() ×(180°﹣60°)=60°,∠ABC=∠EPF=90°,∠PFE=∠EFB=180°﹣90°﹣60°=30°,∴EF=2BE,∴①正确;
×(180°﹣60°)=60°,∠ABC=∠EPF=90°,∠PFE=∠EFB=180°﹣90°﹣60°=30°,∴EF=2BE,∴①正确;
∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴EF⊥BP,∴∠EQB=90°
在△APE和△QEB中
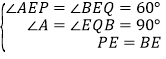
∴△APE≌△QEB,∴②正确;
∵∠EBF=∠EQB=∠BQF=90°,∠BFE=30°,∴∠FBQ=90°﹣30°=60°,∠EBQ=90°﹣60°=30°,∴BE=2QE,EF=2BE,∴EF=4QE,∴FQ=3EQ,∴③正确;
∵BE=4,∠EBF=90°,∠EFB=30°,∴BF=![]() BE=4
BE=4![]() ,∴△BEF的面积为
,∴△BEF的面积为![]() =
=![]() =8
=8![]() .∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴△FPE的面积为8
.∵将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,∴△FPE的面积为8![]() ,∴S四边形BFPE=16
,∴S四边形BFPE=16![]() ,∴④错误。
,∴④错误。
故答案为:①②③.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目