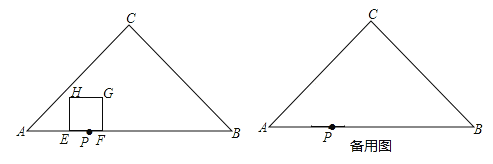题目内容
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.

【答案】(1)![]() ;(2)∠AEC=105°;(3)边BC的长为2或
;(2)∠AEC=105°;(3)边BC的长为2或![]() .
.
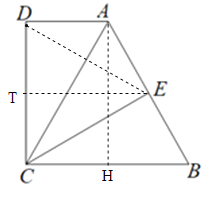
【解析】试题分析:(1)过A作AH⊥BC于H,得到四边形ADCH为矩形.在△BAH中,由勾股定理即可得出结论.
(2)取CD中点T,连接TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∠AET=∠B=70°.
又AD=AE=1,得到∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,即可得到结论.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
解△ABH即可得到结论.
②当∠CAE=90°时,易知△CDA∽△BCA,由相似三角形对应边成比例即可得到结论.
试题解析:解:(1)过A作AH⊥BC于H.由∠D=∠BCD=90°,得四边形ADCH为矩形.
在△BAH中,AB=2,∠BHA=90°,AH=y,HB=![]() ,∴
,∴![]() ,
,
则![]()
(2)取CD中点T,联结TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∴∠AET=∠B=70°.
又AD=AE=1,∴∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,∴∠AEC=70°+35°=105°.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
则在△ABH中,∠B=60°,∠AHB=90°,AB=2,得BH=1,于是BC=2.
②当∠CAE=90°时,易知△CDA∽△BCA,又![]() ,
,
则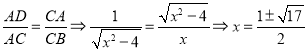 (舍负)
(舍负)
易知∠ACE<90°,所以边BC的长为![]() .
.
综上所述:边BC的长为2或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 | 乙 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过500棵时 | 800元/棵 | 不超过1000棵时 | 800元/棵 |
超过500棵的部分 | 700元/棵 | 超过1000棵的部分 | 600元/棵 |
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?