��Ŀ����
����Ŀ����ͼ��������y=��x2+6x��x�ύ�ڵ�O��A������ΪB������E�������߶Գ����ϣ���F�ڶԳ����Ҳ��������ϣ���C��x���������ϣ���EF ![]()
![]() OC������OE��CF���ı���OCFE��
OC������OE��CF���ı���OCFE��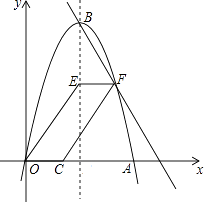
��1����B�����ꣻ
��2����tan��EOC= ![]() ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
��3����0��tan��EOC��3ʱ������ÿһ��ȷ����tan��EOCֵ�������������ı���OCFE�����������������ı��ε����֮��Ϊ1��2ʱ����tan��EOC��
���𰸡�
��1��
�⣺��y=��x2+6x=����x��3��2+9��
��B��3��9��
��2��
�⣺�����ߵĶԳ���Ϊֱ��x=3��ֱ��x=3��x����H����ͼ��
��tan��EOC= ![]() ����tan��EOH=
����tan��EOH= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EH=4��
��E��������3��4����3����4����
��y=4ʱ������x��3��2+9=4�����x1=3�� ![]() ����ȥ����x2=3+
����ȥ����x2=3+ ![]() ��
��
��y=��4ʱ������x��3��2+9=��4�����x1=3�� ![]() ����ȥ����x2=3+
����ȥ����x2=3+ ![]() ��
��
��F��������3+ ![]() ����3+
����3+ ![]() ����4��
����4��
��3��
�⣺��ͼ����ƽ���ı���OEFC��ƽ���ı���OE��F��C��ȸߣ�
���������ı��ε����֮��Ϊ1��2ʱ��OC��=2OC��
��OC=t����OC��=2t��
��F��ĺ�����Ϊ3+t��F���ĺ�����Ϊ3+2t��
����F��F��������껥Ϊ�෴����
�ੁ��3+t��3��2+9+[����3+2t��3��2+9]=0�����t1= ![]() ��t2=��
��t2=�� ![]() ����ȥ����
����ȥ����
��F��������3+ ![]() ��
�� ![]() ����
����
��E��3�� ![]() ����
����
��tan��EOC= ![]() =
= ![]() ��
��
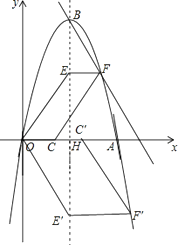
����������1�������䷽����һ��ʽ��ɶ���ʽ���ɵõ�B�����ꣻ��2�������ߵĶԳ���Ϊֱ��x=3��ֱ��x=3��x����H����ͼ���������ж���ɼ����EH���Ӷ��õ�E������Ϊ��3��4����3����4����Ȼ��ֱ���㺯��ֵΪ4�ͩ�4����Ӧ���Ա�����ֵ���ɵõ�����������F������ꣻ��3����ͼ������ƽ���ı���OEFC��ƽ���ı���OE��F��C��ȸߵõ�OC��=2OC�������OC=t����OC��=2t�����ǵõ�F��ĺ�����Ϊ3+t��F���ĺ�����Ϊ3+2t��Ȼ�����õ�F��F��������껥Ϊ�෴�����з��̩���3+t��3��2+9+[����3+2t��3��2+9]=0���ⷽ�����t��ֵ����ɵõ�F������꣬�Ӷ��õ�E�����꣬����������еĶ�����⣮

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��