题目内容
【题目】如图，在
中，
，
，
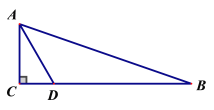
，点D为BC边上一点，且BD=2AD，，求的周长（保留根号）。
【答案】
【解析】
要求△ABC的周长，只要求得BC及AB的长度即可．根据含30°的直角三角形的性质，可以求得AD的长度，也可求得CD的长度；再根据已知条件求得BD的长度，继而求得BC的长度；运用勾股定理可以求得AB的长度，求得△ABC的周长．
解：在Rt△ABC中，∠C=90°，则由勾股定理得AD2=AC2+CD2，
∵∠DAC=30°，
∴AD=2DC，
由AC=
得：DC=1，AD=2，BD=2AD=4，BC=BD+DC=5，
在Rt△ABC中，∠C=90°，AC=，BC=5
由勾股定理得：AB=
，
所以Rt△ABC的周长为AB+BC+AC=2
+5+．
练习册系列答案
相关题目
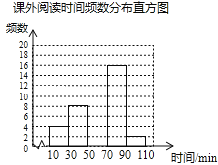
【题目】某学校为了解学生的课外阅读情况，随机抽取了50名学生，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制成如下不完整的统计表．
课外阅读时间t | 频数 | 百分比 |
10≤t＜30 | 4 | 8% |
30≤t＜50 | 8 | 16% |
50≤t＜70 | a | 40% |
70≤t＜90 | 16 | b |
90≤t＜110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题：
（1）a= ，b= ；
（2）将频数分布直方图补充完整；
（3）若全校有900名学生，估计该校有多少学生平均每天的课外阅读时间不少于50min？
【题目】某酒店有三人间、双人间客房若干，各种房型每天的收费标准如下：
普通（元/间） | 豪华（元/间） | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住，选择了一些三人普通间和双人豪华间入住，且恰好住满．已知该旅游团当日住宿费用共计4020元，问该旅游团入住的三人普通间和双人豪华间各为几间？
