��Ŀ����
����Ŀ��ij��˾�������ع���ij������ˮ����ο��ҽ�����ߣ������ضԹ�������3000ǧ�����ϣ���3000ǧ�ˣ������������۷�����������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻أ���֪�ù�˾��ӻ��ص���˾�������Ϊ5000Ԫ��
(1)�ֱ�д���ù�˾���ֹ����ĸ���y��Ԫ�����������ˮ������x��ǧ�ˣ�֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(2)���ݹ������жϣ�ѡ�����ֹ����������٣���˵�����ɣ�
���𰸡���1������������2��������.
��������
����(1)�����ĸ���=��ˮ�����������������ҷ����ĸ���=��ˮ��������������+����ѣ�������������ϵ�ֱ���ʽ���ɣ�(2)�����ҵ����ַ�������ĸ��������бȽϣ��Ӷ�ȷ���������ķ�Χ.
�⣺(1)y��=9x(x��3000)��y��=8x+5000(x��3000)��
(2)��y��=y��ʱ����9x=8x+5000�����x=5000���൱x=5000ǧ��ʱ�����ָ���һ����
��y����y��ʱ����![]() �����3000��x��5000���൱3000��x��5000ʱ��ѡ����ַ��������٣�
�����3000��x��5000���൱3000��x��5000ʱ��ѡ����ַ��������٣�
��y�ף�y��ʱ����x��5000���൱x��5000ǧ��ʱ��ѡ�����ַ��������٣�
������������������С��5000ǧ��ʱ��ѡ�ü��������٣��ڹ���������5000ǧ��ʱ�����ַ�����ͬ���ڹ���������5000ǧ��ʱ��ѡ���ҷ���������.

 ����ѧ��ţ��Ӣ��ϵ�д�
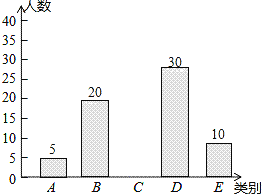
����ѧ��ţ��Ӣ��ϵ�д�����Ŀ���ǽ�����ʱ��������Ż��⣬��������������Զ���ǽ�����һ����Ҫ��ʽ��Ϊ�˽�ijУ���꼶ѧ��ÿ���������������ʱ��������������������100������ѧ�������ݵ������õ���ͼ��ʾ��ͳ��ͼ����
��� | ʱ��t��Сʱ�� | ���� |
A | t��0.5 | 5 |
B | 0.5��t��1 | 20 |
C | 1��t��1.5 | a |
D | 1.5��t��2 | 30 |
E | t��2 | 10 |
�����ͼ����Ϣ����������⣺
��1��a=�� ����
��2����ȫ����ͳ��ͼ��
��3��С��˵������ÿ��Ķ���ʱ���ǵ����������ݵ���λ��������С��ÿ���������������ʱ����ʲô��Χ�ڣ�
��4������ÿ���������������ʱ����1Сʱ���϶�Ϊ������꣬���ѧ���Ĵ�����Ƕ��٣�