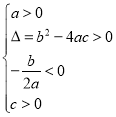题目内容
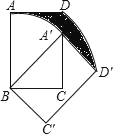
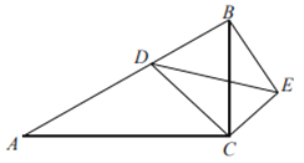
【题目】如图,在![]() 中
中![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 与
与![]() 相切于点
相切于点![]() ,在
,在![]() 边上取一点
边上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() ,
,![]() 时,求
时,求![]() 的半径.
的半径.
【答案】(1)直线![]() 与
与![]() 相切,理由见解析;(2)
相切,理由见解析;(2)![]() 的半径为1.
的半径为1.
【解析】
(1)如图(见解析),先根据圆的切线的性质、中位线定理得出![]() 的半径OE等于CD,再根据三角形全等的判定定理与性质可得
的半径OE等于CD,再根据三角形全等的判定定理与性质可得![]() ,然后由圆的切线的判定即可得;
,然后由圆的切线的判定即可得;
(2)设![]() 的半径为
的半径为![]() ,则
,则![]() ,先根据线段中点的定义得出
,先根据线段中点的定义得出![]() ,再根据勾股定理可得AC的长,然后根据中位线定理可得OD的长,最后在
,再根据勾股定理可得AC的长,然后根据中位线定理可得OD的长,最后在![]() 中利用勾股定理即可得.
中利用勾股定理即可得.
(1)直线![]() 与
与![]() 相切,理由如下:
相切,理由如下:
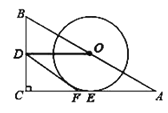
如图,连接OE,过点O作![]() 于点P
于点P
![]() 相切
相切![]() 于点
于点![]()
![]() ,OE为
,OE为![]() 的半径
的半径
![]() 点
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
![]()
![]()
![]() 四边形ODCE是矩形
四边形ODCE是矩形
![]()
在![]() 和
和![]() 中,
中,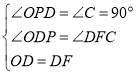
![]()
![]()
![]() ,即OP为
,即OP为![]() 的半径
的半径
则直线![]() 与
与![]() 相切;
相切;
(2)设![]() 的半径为
的半径为![]() ,则
,则![]()
![]() 点
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
由(1)已证:![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
故![]() 的半径为1.
的半径为1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A、B城往C、D两乡运肥料的平均费用如下表. 现C乡需要肥料240吨,D乡需要肥料260吨.
A城(出) | B城(出) | |
C乡(人) | 20元/吨 | 15元/吨 |
D乡(人) | 25元/吨 | 30元/吨 |
(1)A城和B城各多少吨肥料?
(2)设从B城运往D乡肥料x吨,总运费为y元,求y与x之间的函数关系,并写出自变量x的取值范围;
(3)由于更换车型,使B城运往D乡的运费每吨减少a元(a>0),其余路线运费不变,若C、D两乡的总运费最小值不少于10040元,求a的最大整数值.
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
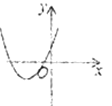
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.