Question

【题目】如图,AB为半圆O的直径,AB=2,C,D为半圆上两个动点(D在C右侧),且满足∠COD=60°,连结AD,BC相交于点P若点C从A出发按顺时针方向运动,当点D与B重合时运动停止,则点P所经过的路径长为______.

Answer 1

【答案】

【解析】连结CO,根据同弧所对的圆周角相等可得∠3=∠4，由△OCD为等边三角形，可得∠APB=120°为定角，AB为定长=2，作等边三角形可得点P运动的轨迹⊙M上的弧 (红色部分)，从而求解.

连结CO,

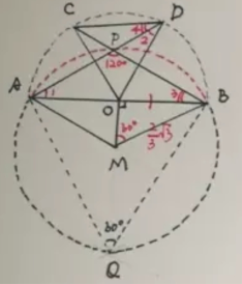
∵OA=OD, ∴∠1=∠2, ∵,∴∠3=∠4, ∵∠COD=60°,OC=OD, ∴△OCD为等边三角形，∴∠2+∠4=60°，即∠1+∠3=60°, ∴∠APB=180°-(∠1+∠3)=120°, ∴∠APB=120°为定角，AB为定长=2，作等边三角形ABQ,再作等边三角形ABQ的外接圆⊙M,则点P运动的轨迹⊙M上的弧 (红色部分)易知∠OMB=60°,OB=1, ∴BM= ，∴运动路径长为.故答案为：.