Question

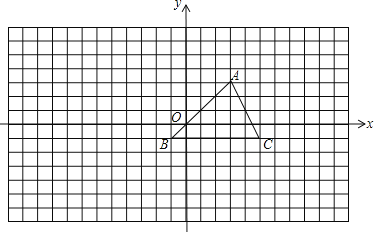
【题目】如图，一次函数的图象与反比例函数的图象交于、两点，点的横坐标为，点的横坐标为，.

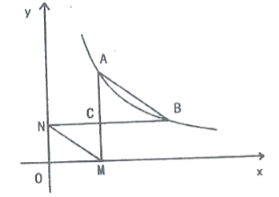
（1）点的纵坐标为___________;

（2）作轴，轴，垂足分别为、，与相交于点，连结.

①求证：；

②若四边形是正方形且面积为，把直线向右平移个单位，平移后的直线与反比例函数的图象交于点，与轴交于点，求的值.

Answer 1

【答案】（1）；（2）证明见解析；（3）16

【解析】

(1)由点A的横坐标,利用反比例函数图象上点的坐标特征可求出点A的纵坐标

(2)①由反比例函数图象上点的坐标特征可得出点A,B的坐标,进而可得出MC,NC,BC,AC的长度,由长度之间的关系可得出,结合∠ACB=∠MCN=90°可证出△ACB∽△MCN,利用相似三角形的性质可得出∠ABC=∠MNC,再利用“内错角相等,两直线平行”可证出AB∥MN

②由正方形的性质结合反比例函数图象上点的坐标特征,可得出点A,C的坐标及k值,由点C的坐标可得出直线OC的解析式,利用平移的性质可求出直线PQ的解析式及点Q的坐标,联立直线PQ和反比例函数解析式成方程组,通过解方程组可求出点P的坐标,再利用两点间的距离公式可求出的值

解：（1）当时，，

∴点A的纵坐标为，

故答案为：

（2）①证明：当时，，

∴点B的坐标为

∵AM⊥x轴，BN⊥y轴

∴点C的坐标为，

∴NC=m，BC=n-m，MC=，AC=，

∴，；

∴

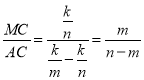又∵∠ACB=∠MCN=90°

∴△ACB∽△MCN

∴∠ABC=∠MNC

∴AB∥MN

②∵四边形ABMN是正方形,

∴CM=CN， BN=2CN， AM=2CM

∴n=2m，△CMN为等腰直角三角形

∵

∴

∴CM=CN=2

∴m=2，n=4

∴点A的坐标为(2,4)，点C的坐标为(2,2)

∴k=2×4=8，直线OC的解析式为y=x.

∵把直线OC向右平移c个单位得到直线PQ

∴直线PQ的解析式为y=x-c,点Q的坐标为(c,0)

联立直线PQ和反比例函数解析式成方程组得：，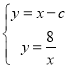

解得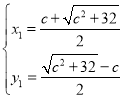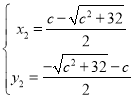：， （舍去）

∴点P的坐标为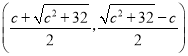

∴

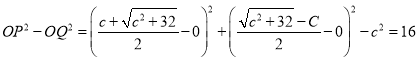
故答案为：16