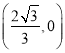题目内容
【题目】在
中，
，点
为直线
上一动点（点不与点
重合），以
为腰作等腰直角
，使
，连接
．
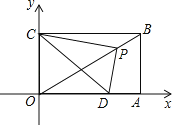
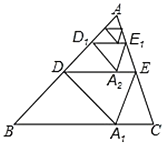
（1）观察猜想
如图1，当点在线段上时，
①与的位置关系为__________；
②
之间的数量关系为___________（提示：可证
）
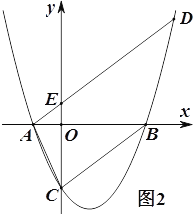
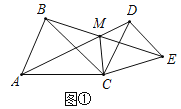
（2）数学思考
如图2，当点在线段
的延长线上时，（1）中的①、②结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；
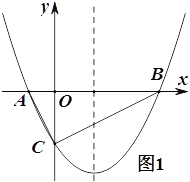
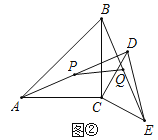
（3）拓展延伸
如图3，当点在线段的延长线时，将沿线段
翻折，使点
与点
重合，连接
，若
，请直接写出线段
的长．（提示：做
于
，做
于
）
【答案】（1）①BC⊥CF；②BC＝CF＋DC；（2）C⊥CF成立；BC＝CF＋DC不成立，正确结论：DC＝CF＋BC，证明详见解析；（3）
【解析】
（1）①根据正方形的性质得，∠BAC＝∠DAF＝90°，推出△DAB≌△FAC（SAS）；②由正方形ADEF的性质可推出△DAB≌△FAC，根据全等三角形的性质可得到
，
，根据余角的性质即可得到结论；
（2）根据正方形的性质得到∠BAC＝∠DAF＝90°，推出△DAB≌△FAC，根据全等三角形的性质以及等腰三角形的角的性质可得到结论；
（3）过A作
于H，过E作
于M，证明
，推出
，
，推出
，即可解决问题．
（1）①正方形ADEF中，
∵
∴
在△DAB与△FAC中
∴
∴
∴
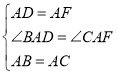
，即
；
②∵
∴
∵
∴
（2）BC⊥CF成立；BC＝CF＋DC不成立，正确结论：DC＝CF＋BC
证明：∵△ABC和△ADF都是等腰直角三角形
∴AB＝AC，AD＝AF，∠BAC＝∠DAF＝90°，
∴∠BAD＝∠CAF
在△DAB和△FAC中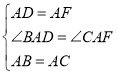
∴△DAB≌△FAC（SAS）
∴∠ABD＝∠ACF，DB＝CF
∵∠BAC＝90°，AB＝AC，
∴∠ACB＝∠ABC＝45°
∴∠ABD＝180°－45°＝135°
∴∠ACF＝∠ABD＝135°
∴∠BCF＝∠ACF－∠ACB＝135°－45°＝90°，
∴CF⊥BC
∵CD＝DB＋BC，DB＝CF
∴DC＝CF＋BC
（3）过A作 于H，过E作 于M，
∵
，
∴
∴
∴
∵四边形ADEF是正方形
∴
∵
∴四边形CMEN是矩形
∴
∵
∴
∴
在△ADH和△DEM中
∴
∴
∴
∴
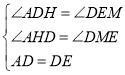
