题目内容
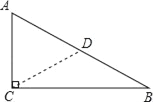
【题目】如图1,![]() ,
,![]() ,
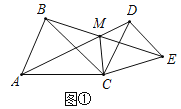
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
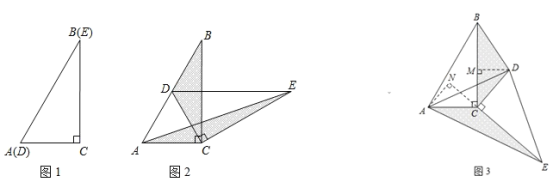
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 为等腰直角三角形,证明见解析.
为等腰直角三角形,证明见解析.
【解析】
分析(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
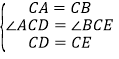 ,
,
![]() ≌
≌![]()
![]() ;
;
![]() 如图1,
如图1,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 中,
中,![]() ;
;
![]() 为等腰直角三角形.
为等腰直角三角形.
证明:如图2,由![]() 可得,
可得,![]() ,
,
![]() ,BE的中点分别为点P、Q,
,BE的中点分别为点P、Q,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ,
,
![]() ,且
,且![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形.
为等腰直角三角形.

【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
【题目】近期江苏省各地均发布“雾霾”黄色预警,我市某口罩厂商生产一种新型口罩产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系满足下表.
销售单价x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 20 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示y与x的变化规律,并直接写出y与x之间的函数关系式为__________;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?