题目内容
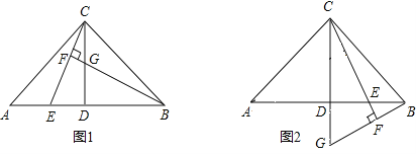
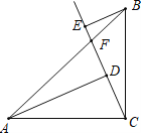
【题目】 如图,在△ABC中,∠ACB=90°,AC=BC过点C的射线CF交边AB于点F,AD⊥CF于点D,BE⊥CF于点E,AD=3,BE=1.
(1)求证:△ADC≌△CEB.
(2)求DE的长.
【答案】(1)见解析;(2)2
【解析】
(1)易证∠CAD=∠BCE,即可证明△ACD≌△BCE;
(2)利用全等三角形的性质即可解决问题.
(1)证明:∵∠ACB=90°,AD⊥CF
∴∠BCE+∠ACD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
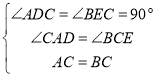 ,
,
∴△ADC≌△CEB(AAS);
(2)解:∵△ADC≌△CEB,
∴CD=BE,AD=CE,
∵AD=3,BE=1,
∴DE=CE-CD= AD - BE =2.

练习册系列答案
相关题目
【题目】从一定高度落下的图钉,落地后可能图钉针尖着地.也可能图钉针尖不着地,雨薇同学在相同条件下做了这个实验.并将数据记录如下:
实验次数n | 200 | 400 | 600 | 800 | 1000 | … |
针尖着地频数m | 84 | 176 | 280 | 362 | 451 | … |
针尖着地频率 | 0.420 | 0.440 | 0.467 | 0.453 | 0.451 | … |
(1)观察针尖着地的频率是否稳定,若稳定,请写针尖着地频率的常数______(精确到0.01);若不稳定,请说明理由.
(2)假如小明同学在相同条件下做了此实验10000次,估计图钉针尖着地的次数大约是多少.