��Ŀ����
����Ŀ������ѧ���ϣ���ʦҪ��ѧ��̽���������⣺
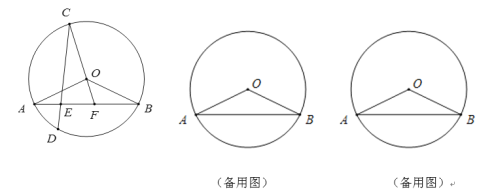
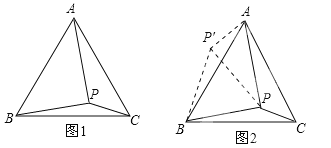
(1)��ͼ1���ڵȱ�������ABC����һ��P����PA=2��PB=![]() ��PC=1�������BPC�Ķ���.�ͬѧһʱû��˼·���������������Ŀ��Ϣ������PA��PB��PC�ij�Ϊ�߹��ɵ���������ֱ�������Σ���ͻȻ������ȷ��˼·����ͼ2������BPC�Ƶ�B��ʱ����ת60�����õ���BP��A������PP�����á�P��PB�ǵȱ������Σ���PP��A��ֱ��������.���BPC=_______��.
��PC=1�������BPC�Ķ���.�ͬѧһʱû��˼·���������������Ŀ��Ϣ������PA��PB��PC�ij�Ϊ�߹��ɵ���������ֱ�������Σ���ͻȻ������ȷ��˼·����ͼ2������BPC�Ƶ�B��ʱ����ת60�����õ���BP��A������PP�����á�P��PB�ǵȱ������Σ���PP��A��ֱ��������.���BPC=_______��.
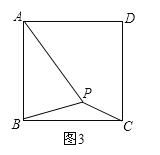
(2)��ͼ3����������ABCD����һ��P����PA=![]() ��BP=
��BP=![]() ��PC=1�������BPC�Ķ���.
��PC=1�������BPC�Ķ���.
(3)��ͼ3�У�����������ABCD������һ��Q��QA=a��QB=b��QC=c(a>b��a>c)���Բ���a��b��c����ʲô����ʱ����BQC�Ķ������(2)���С�BPC�Ķ�����ȣ���ֱ��д������.
���𰸡���1��150������2����BPC��135������3��a2��c2+2b2��
��������
��1����������֤�á�P��PB���������Σ���P��PA��ֱ�������Σ������ɵá�BP'P���AP'P�Ķ������ٸ�����ת�����ʼ��ý����
��2�����գ�1����˼·������BPC�Ƶ�B��ʱ����ת90�����õ���BP'A��Ȼ������PP'��������ת�����ʿɵá�![]() �ǵ���ֱ�������Σ����ݹ��ɶ������涨���ɵá�AP'P��90�����Ӷ��ɵý��ۣ�
�ǵ���ֱ�������Σ����ݹ��ɶ������涨���ɵá�AP'P��90�����Ӷ��ɵý��ۣ�
��3�����գ�2����˼·������BQC�Ƶ�B��ʱ����ת90�����õ���BQ'A��Ȼ������QQ'��������ת�����ʿɵá�![]() �ǵ���ֱ�������Σ���һ�����á�AQ'Q��90����Ȼ����ݹ��ɶ������ɵó����ۣ�
�ǵ���ֱ�������Σ���һ�����á�AQ'Q��90����Ȼ����ݹ��ɶ������ɵó����ۣ�
�⣺��1���߽���BPC�Ƶ�B��ʱ����ת60�����õ���BP��A��
��BP= BP������PBP'��60����
���P��PB�ǵȱ������Σ�
���BP'P��60����
��PA=2��PP'= BP=![]() ��PC=P��A=1��
��PC=P��A=1��
��![]() ��
��
���P��PA��ֱ�������Σ���AP'P��90����
���AP'B��150����
���BPC����AP'B��150����
�ʴ�Ϊ��150����
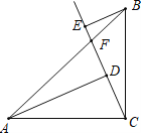
��2����ͼ4������BPC�Ƶ�B��ʱ����ת90�����õ���BP'A������PP'��
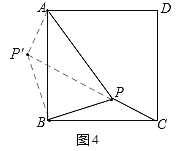
��BP��BP'��![]() ����PBP'��90����PC��P'A����AP'B����BPC��
����PBP'��90����PC��P'A����AP'B����BPC��
���BP'P��45����PP'��![]() ��2��
��2��
��P'P2+P'A2��5��PA2��5��
��P'P2+P'A2��PA2��
���AP'P��90����
���AP'B����AP'P+��BP'P��135����
�ߡ�AP'B����BPC��
���BPC��135����
��3����ͼ5������BQC�Ƶ�B��ʱ����ת90�����õ���BQ'A������QQ'��
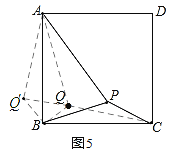
��BQ��BQ'��b����QBQ'��90������AQ'B����BQC��135����QC��AQ'��c��
��QQ'��![]() b����BQ'Q��45����
b����BQ'Q��45����
���AQ'Q����AQ'B����BQ'Q��90����
��AQ2��Q'A2+Q'Q2��
��a2��c2+2b2��

����Ŀ���������ij�̳��ӳ����������ӻ��������ۣ������۸������ۼ۸����±���
���ӻ��ͺ� | �� | �� |
������(Ԫ/̨) | 1500 | 2500 |
���ۼ�(Ԫ/̨) | 2025 | 3640 |
���̳������ס��������ͺŵĵ��ӻ���50̨����ȥ9��Ԫ��
(1)���̳������ס����ͺŵĵ��ӻ�������̨��
(2)ӭ��Ԫ�����̳����������Żݴ����������ۼ۵����������������ͺŵ��ӻ������ֵ��ӻ�������ϣ��̳�������8.5%��������ͺŵ��ӻ��������ۣ�