题目内容
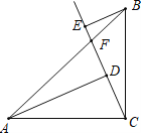
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上的一动点.连接CE,过点B作BF⊥CE,垂足为F交直线CD于点G.
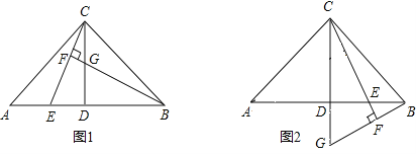
(1)如图l,当点E在线段AD上时,请直接判断AE与CG的数量关系;
(2)如图2,当点E在线段DB上时,(1)中AE与CG的数量关系是否依然成立,若成立,请证明;若不成立,请说明理由.
(3)当AC=2![]() ,且四边形DEFG的面积为
,且四边形DEFG的面积为![]() 时,请直接写出线段AE的长.
时,请直接写出线段AE的长.
【答案】(1)AE=CG,理由见解析;(2)依然成立, AE=CG;理由见解析;(3)线段AE的长为1或3.
【解析】
(1)根据等腰直角三角形的性质得到∠A=∠ABC,根据同角的余角相等得到∠CBG=∠ACE,根据ASA证明△ACE≌△CBG,即可得出结论;
(2)同理即可证明△ACE≌△CBG,即可得出结论;
(3)由等腰直角三角形的性质得出AB=![]() AC=4,CD=
AC=4,CD=![]() AB=AD=BD=2,CD⊥AB,证明△CDE≌△BDG,得出DE=DG,设DE=DG=x,则CG=2-x,CE=
AB=AD=BD=2,CD⊥AB,证明△CDE≌△BDG,得出DE=DG,设DE=DG=x,则CG=2-x,CE=![]() ,证明△CFG∽△CDE,得出
,证明△CFG∽△CDE,得出![]() ,求出FG=
,求出FG=![]() ,CF=
,CF=![]() ,,由四边形DEFG的面积=△CDE的面积-△CFG的面积=
,,由四边形DEFG的面积=△CDE的面积-△CFG的面积=![]() ,得出方程,解方程得出DE=1;再分两种情况,即可得出答案.
,得出方程,解方程得出DE=1;再分两种情况,即可得出答案.
(1)AE=CG,理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,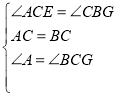 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(2)(1)中AE与CG的数量关系依然成立,即AE=CG;理由如下:
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,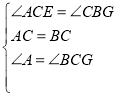 ,
,
∴△ACE≌△CBG(ASA),
∴AE=CG;
(3)∵在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,
∴AB=![]() AC=4,CD=
AC=4,CD=![]() AB=AD=BD=2,CD⊥AB,
AB=AD=BD=2,CD⊥AB,
∴∠CDE=∠BDG=90°,
∴∠CED+∠DCE=90°,
∵BF⊥CE,
∴∠DBG+∠CED=∠90°,
∴∠DCE=∠DBG,
在△CDE和△BDG中,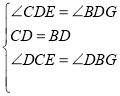 ,
,
∴△CDE≌△BDG(ASA),
∴DE=DG,
设DE=DG=x,则CG=2-x,CE=![]() =
=![]() ,
,
∵∠CFG=∠CDE=90°,∠FCG=∠DCE,
∴△CFG∽△CDE,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:FG=![]() ,CF=
,CF=![]() ,
,
∵四边形DEFG的面积=△CDE的面积-△CFG的面积=![]() ,
,
∴![]() ×x×2-
×x×2-![]() ×
×![]() ×
×![]() =
=![]() ,
,
解得:x=1,即DE=1;
①当点E在线段AD上时,AE=AD-DE=1;
②当点E在线段DB上时,AE=AD+DE=3;
综上所述,当AC=2![]() ,且四边形DEFG的面积为
,且四边形DEFG的面积为![]() 时,线段AE的长为1或3.
时,线段AE的长为1或3.

 阅读快车系列答案
阅读快车系列答案