题目内容
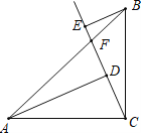
【题目】如图，在河流两边有甲、乙两座山，现在从甲山A处的位置向乙山B处拉电线，已知甲山AC的坡比为15：8.乙山BD的坡比为4：3，甲山上A点到河边c的距离AC＝340米，乙山上B点到河边D的距离BD＝900米，从B处看A处的俯角为26°，则河CD的宽度是（参考值：sin26°＝0.4383，tan26°＝0.4788，co26°＝0.8988）结果精确到0.01）（ ）
A.177.19米B.188.85米C.192.0米D.258.25米
【答案】A
【解析】
由此题已知线段和角度，求其它线段的长度可知，本题考查解直角三角形问题；需构造直角三角形，由已知条件AC的坡比为15：8.可知，需以AC为斜边构造直角三角形，同理需以BD为斜边构造直角三角形；由已知条件从B处看A处的俯角为26°可知，需以AB为斜边构造直角三角形.
过点A、B分别作CD的垂线段AE、BF，过点B作BF的垂线BM交EA的延长线于M，则得到三个直角三角形；
由AC的坡比为15：8，设
，
在直角
中，
，
，解得
；
于是
；
同理可得：
；
；
在直角
中，
，
；
，即
；
；
.
故选：A.
练习册系列答案
相关题目
