题目内容
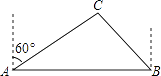
【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.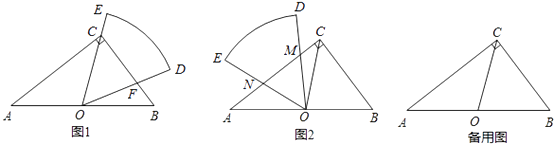
(1)证明△COF是等腰三角形,并求出CF的长;
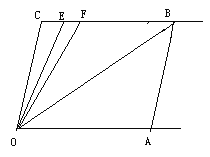
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
【答案】
(1)解:∵∠ACB=90°,点O是AB的中点,
∴OC=0B=OA=5.
∴∠OCB=∠B,∠ACO=∠A.
∵∠DOE=∠B,
∴∠FOC=∠OCF.
∴FC=FO.
∴△COF是等腰三角形.
过点F作FH⊥OC,垂足为H,如图1,
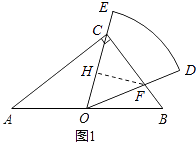
∵FC=FO,FH⊥OC,
∴CH=OH= ![]() ,∠CHF=90°.
,∠CHF=90°.
∵∠HCF=∠B,∠CHF=∠BCA=90°,
∴△CHF∽△BCA.
∴ ![]() =
= ![]() .
.
∵CH= ![]() ,AB=10,BC=6,
,AB=10,BC=6,
∴CF= ![]() .
.
∴CF的长为 ![]() .
.
(2)解:①若△OMN∽△BCO,如图2,
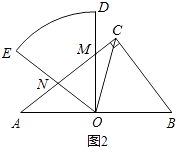
则有∠NMO=∠OCB.
∵∠OCB=∠B,
∴∠NMO=∠B.
∵∠A=∠A,
∴△AOM∽△ACB.
∴ ![]() =
= ![]() .
.
∵∠ACB=90°,AB=10,BC=6,
∴AC=8.
∵AO=5,AC=8,AB=10,
∴AM= ![]() .
.
∴CM=AC﹣AM= ![]() .
.
②若△OMN∽△BOC,如图3,
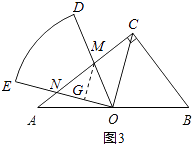
则有∠MNO=∠OCB.
∵∠OCB=∠B,
∴∠MNO=∠B.
∵∠ACO=∠A,
∴△CON∽△ACB.
∴ ![]() =
= ![]() =
= ![]() .
.
∵BC=6,AB=10,AC=8,CO=5,
∴ON= ![]() ,CN=
,CN= ![]() .
.
过点M作MG⊥ON,垂足为G,如图3,
∵∠MNO=∠B,∠MON=∠B,
∴∠MNO=∠MON.
∴MN=MO.
∵MG⊥ON,即∠MGN=90°,
∴NG=OG= ![]() .
.
∵∠MNG=∠B,∠MGN=∠ACB=90°,
∴△MGN∽△ACB.
∴ ![]() =
= ![]() .
.
∵GN= ![]() ,BC=6,AB=10,
,BC=6,AB=10,
∴MN= ![]() .
.
∴CM=CN﹣MN= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∴当CM的长是 ![]() 或
或 ![]() 时,△OMN与△BCO相似.
时,△OMN与△BCO相似.
【解析】(1)在直角三角形中由∠ACB=90°,点O是AB的中点,得到OC=0B=OA,∠OCB=∠B,∠ACO=∠A,由∠DOE=∠B,得到∠FOC=∠OCF,由等角对等边得到FC=FO,即△COF是等腰三角形;由FC=FO,FH⊥OC,得到CH=OH ,由∠HCF=∠B,∠CHF=∠BCA,得到△CHF∽△BCA,得到 比例,求出CF的长;(2)①若△OMN∽△BCO,则有对应角相等,即∠NMO=∠OCB,由∠OCB=∠B,得到∠NMO=∠B;再由∠A=∠A,得到△AOM∽△ACB,![]() 根据勾股定理由∠ACB=90°,求出AC=8,得到AM的值,即CM=AC﹣AM;②若△OMN∽△BOC,则有对应角相等∠MNO=∠OCB,由∠OCB=∠B,得到∠MNO=∠B,又因为∠ACO=∠A,所以△CON∽△ACB,得
根据勾股定理由∠ACB=90°,求出AC=8,得到AM的值,即CM=AC﹣AM;②若△OMN∽△BOC,则有对应角相等∠MNO=∠OCB,由∠OCB=∠B,得到∠MNO=∠B,又因为∠ACO=∠A,所以△CON∽△ACB,得![]() 到比例,求出ON
到比例,求出ON![]() 、CN的值;由∠MNO=∠MO,得到MN=MO,因为MG⊥ON,得到NG=OG,因为∠MNG=∠B,∠MGN=∠ACB,得到△MGN∽△ACB,得到比例 ,求出MN的值,得到CM=CN﹣MN,求出当CM的长是
、CN的值;由∠MNO=∠MO,得到MN=MO,因为MG⊥ON,得到NG=OG,因为∠MNG=∠B,∠MGN=∠ACB,得到△MGN∽△ACB,得到比例 ,求出MN的值,得到CM=CN﹣MN,求出当CM的长是 ![]() 或
或 ![]() 时,△OMN与△BCO相似.
时,△OMN与△BCO相似.
【考点精析】认真审题,首先需要了解直角三角形斜边上的中线(直角三角形斜边上的中线等于斜边的一半),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案