题目内容
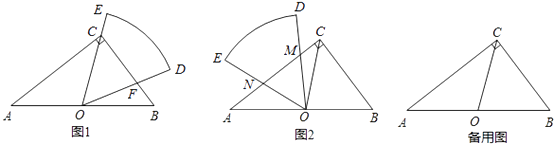
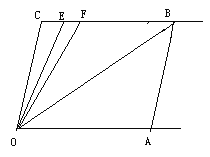
【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
【答案】(1)30°;(2)1:2;(3)45°.
【解析】
(1)根据两直线平行,同旁内角互补求出∠AOC,再根据角平分线的定义求出∠EOB=![]() ∠AOC,代入数据即可得解;
∠AOC,代入数据即可得解;
(2)根据两直线平行,内错角相等可得∠OBC=∠BOA,从而得到∠OBC=∠FOB,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OFC=2∠OBC,从而得解;
(3)设∠AOB=x,根据两直线平行,内错角相等表示出∠CBO=∠AOB=x,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC,然后利用三角形的内角和等于180°列式表示出∠OBA,然后列出方程求解即可.
(1)∵CB∥OA,∴∠AOC=180°-∠C=180°-120°=60°.
∵∠FOB=∠AOB,OE平分∠COF,∴∠EOB=![]() ∠AOC=
∠AOC=![]() ×60°=30°;
×60°=30°;
(2)∠OBC:∠OFC的值不会发生变化,为1:2.
∵CB∥OA,∴∠OBC=∠BOA.
∵∠FOB=∠AOB,∴∠OBC=∠FOB,∴∠OFC=∠OBC+∠FOB=2∠OBC,∴∠OBC:∠OFC=1:2;
(3)当平行移动AB至∠OBA=45°时,∠OEC=∠OBA.
设∠AOB=x.
∵CB∥AO,∴∠CBO=∠AOB=x.
∵∠OEC=∠CBO+∠EOB=x+30°,∠OBA=180°-∠A-∠AOB=180°-120°-x=60°-x,∴x+30°=60°-x,∴x=15°,∴∠OEC=∠OBA=60°-15°=45°.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
【题目】在一次试验中,小明把一根弹簧的上端固定,在其下端悬挂物体,测得弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系如下表:
之间的关系如下表:
所挂物体质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 8 | 10 | 12 | 14 | 16 | 18 |
下列说法错误的是( )
A.弹簧的长度随所挂物体质量的变化而变化,所挂物体质量是自变量,弹簧长度是因变量
B.不挂物体时,弹簧的长度为![]()
C.弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系式是
之间的关系式是![]()
D.在弹性限度内,当所挂物体的质量为![]() 时,弹簧的长度为
时,弹簧的长度为![]()