题目内容
【题目】计算下列各式：
（1）解不等式
，并把它的解集在数轴上表示出来．
（2）解方程组：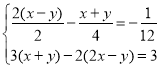
．
【答案】（1）x＜
，数轴见解析；（2）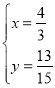
【解析】
（1）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
（2）先整理为一般式，再利用加减消元法求解可得．
解：
（1）去分母得：6（1﹣2x）﹣4（3x+2）＞﹣3（7x+3），
去括号得，6﹣12x﹣12x﹣8＞﹣21x﹣9，
移项得，﹣12x﹣12x+21x＞﹣9﹣6+8，
合并同类项得，﹣3x＞﹣7，
系数化为1得，x＜，
在数轴上表示不等式的解集为：
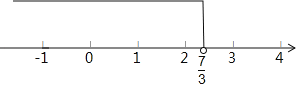
（2）原方程组可化为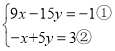
，
由②×3得，﹣3x+15y＝9③，
③+①得，6x＝8，
解得
，
把代入③得，
，
解得y
，
∴原方程组的解是．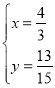
练习册系列答案
特高级教师点拨系列答案
文敬图书课时先锋系列答案
相关题目
【题目】在一次试验中，小明把一根弹簧的上端固定，在其下端悬挂物体，测得弹簧的长度
与所挂物体的质量
之间的关系如下表：
所挂物体质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 8 | 10 | 12 | 14 | 16 | 18 |
下列说法错误的是（ ）
A.弹簧的长度随所挂物体质量的变化而变化，所挂物体质量是自变量，弹簧长度是因变量
B.不挂物体时，弹簧的长度为
C.弹簧的长度与所挂物体的质量之间的关系式是
D.在弹性限度内，当所挂物体的质量为
时，弹簧的长度为
