题目内容
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
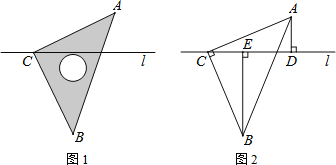
(1)△ACD与△CBE全等吗?说明你的理由.
(2)猜想线段AD、BE、DE之间的关系.(直接写出答案)
【答案】(1)详见解析;(2)AD=BE-DE;
【解析】
(1)观察图形,结合已知条件,可知全等三角形为:△ACD与△CBE.根据AAS即可证明;
(2)由(1)知△ACD≌△CBE,根据全等三角形的对应边相等,得出CD=BE,AD=CE,从而求出线段AD、BE、DE之间的关系.
证明:(1)∵AD⊥CD,BE⊥CD,
∴∠ADC=∠CEB=90°,
又∵∠ACB=90°,
∴∠ACD=∠CBE=90°-∠ECB.
在△ACD与△CBE中, ,
,
∴△ACD≌△CBE(AAS);
(2)AD=BE-DE,理由如下:
∵△ACD≌△CBE,
∴CD=BE,AD=CE,
又∵CE=CD-DE,
∴AD=BE-DE.

练习册系列答案
相关题目