题目内容
【题目】如图,等腰△ABC,点D、E、F分别在BC、AB、AC上,且∠BAC=∠ADE=∠ADF=60°.
(1)在图中找出与∠DAC相等的角,并加以证明;
(2)若AB=6,BE=m,求:AF(用含m的式子表示).
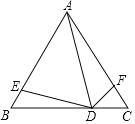
【答案】(1)∠BDE=∠DAC,证明见解析;(2)AF=6﹣m.
【解析】
(1)首先证明△ABC是等边三角形,再利用三角形的外角的性质解决问题即可.
(2)在DE上截取DG=DF,连接AG,先判定△ADG≌△ADF,得到AG=AF,再根据∠AEG=∠AGE,得出AE=AG,进而得到AE=AF即可解决问题.
解:(1)结论:∠BDE=∠DAC.
理由:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠C=60°.
∵∠ADB=∠3+∠ADE=∠1+∠C,∠ADE=∠C=60°,
∴∠3=∠1.
(2)如图,在DE上截取DG=DF,连接AG.

∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵∠ADE=∠ADF=60°,AD=AD,
∴△ADG≌△ADF(SAS),
∴AG=AF,∠1=∠2.
∵∠3=∠1,
∴∠3=∠2
∵∠AEG=60°+∠3,∠AGE=60°+∠2,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=AF=6﹣m.

练习册系列答案
相关题目