题目内容
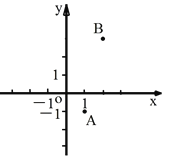
【题目】如图，已知点A（1，-1），B（2，3），点P为x轴上一点，当|PA-PB|的值最大时，点P的坐标为（ ）
A.（-1，0）B.（
，0）C.（
，0）D.（1，0）
【答案】B
【解析】
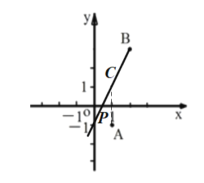
由题意作A关于x轴对称点C，连接BC并延长，BC的延长线与x轴的交点即为所求的P点；首先利用待定系数法即可求得直线BC的解析式，继而求得点P的坐标．
解：作A关于x轴对称点C，连接BC并延长交x轴于点P，
∵A（1，-1），
∴C的坐标为（1， 1），
连接BC，设直线BC的解析式为：y=kx+b，
∴
,解得
，
∴直线BC的解析式为：y=2x-1，
当y=0时，x=
，
∴点P的坐标为：（，0），
∵当B，C，P不共线时，根据三角形三边的关系可得：|PA-PB|=|PC-PB|＜BC，
∴此时|PA-PB|=|PC-PB|=BC取得最大值．
故选：B．
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息，完成下列各题：
（1）当x=3时，y=________；
（2）当x=_____时，y有最________值为________；
（3）若点A（x1，y1）、B（x2，y2）是该二次函数图象上的两点，且﹣1＜x1＜0，1＜x2＜2，试比较两函数值的大小：y1________y2 ；
（4）若自变量x的取值范围是0≤x≤5，则函数值y的取值范围是________．