Question

【题目】阅读理解

在平面直角坐标系xoy中，两条直线l1：y=k1x+b1（k1≠0），l2：y=k2x+b2（k2≠0），①当l1∥l2时，k1=k2，且b1≠b2；②当l1⊥l2时，k1·k2=－1．

类比应用

（1）已知直线l：y=2x－1，若直线l1：y=k1x+b1与直线l平行，且经过点A（－2，1），试求直线l1的表达式；

拓展提升

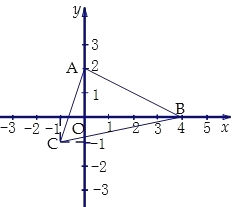
（2）如图，在平面直角坐标系xoy中，△ABC的顶点坐标分别为：A（0，2），B（4，0），C（－1，－1），试求出AB边上的高CD所在直线的表达式．

Answer 1

【答案】（1）y=2x+5；（2）y=2x+1．

【解析】

（1）利用平行线性质可知k值相等，进而将P点坐标代入l1即可求出直线l1的表达式；

（2）由题意设直线AB的表达式为：y=kx+b，求出直线AB的表达式，再根据题意设AB边上的高CD所在直线的表达式为：y=mx+n，进行分析求出CD所在直线的表达式.

解：（1）∵l1∥l，

∴k1=2，

∵直线经过点P（-2，1），

∴1=2×（-2）+b1，b1=5，

∴直线l1表达式为：y=2x+5.

（2）设直线AB的表达式为：y=kx+b

∵直线经过点A（0，2），B（4，0），

∴， 解得：，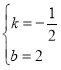

∴直线AB的表达式为：;

设AB边上的高CD所在直线的表达式为：y=mx+n，

∵CD⊥AB，

∴m·（）=－1，m=2，

∵直线CD经过点C（-1，-1），

∴-1=2×（-1）+n，n=1，

∴AB边上的高CD所在直线的表达式为：y=2x+1.