��Ŀ����
����Ŀ��ij��Ʒ�������۽���Ϊ40Ԫ/���ƻ�����г����鷢�֣�����ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣬��ÿ��ƻ�������ۼ�Ϊx��Ԫ����x��50��ʱ��ƽ��ÿ�����������Ϊw��Ԫ��.
��1����w��x֮��ĺ�����ϵʽ��
��2����ÿ��ƻ�������ۼ�Ϊ����Ԫʱ�����Ի����������������Ϊ����Ԫ��
��3���ٽ����ڣ�Ϊ�ȶ��г�����۲��Ź涨ÿ��ƻ���ۼ۲��ø���58Ԫ�����ʱƽ��ÿ���õ���������Ƕ���Ԫ��
���𰸡���1��w��x֮��ĺ�����ϵʽΪw=![]() ��
��
��2��ÿ��ƻ�������ۼ�Ϊ60Ԫʱ�����Ի������������������1200Ԫ��
��3����x=58ʱ��w�����ֵ��w���=1188����ʱƽ��ÿ���õ����������1188Ԫ��
��������
��1�����������ó�ƽ��ÿ����������y�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽΪy��903��x50����Ȼ������������������������ۼ����ۣ����г�ƽ��ÿ�����������w��Ԫ�������ۼ�x��Ԫ/�䣩֮��ĺ�����ϵʽ���ɣ�
��2��������������Ա�����ȡֵ��Χ��Ȼ�������1���ж��κ�������ֵ���ɣ�
��3�������������x��ȡֵ��Χ�������ö��κ������������ɵã�
�⣺��1��������ã�y��903��x50����
��w=![]() =
=![]() =
=![]() ��
��
��w��x֮��ĺ�����ϵʽΪw=![]() ��
��
��2����![]() ����
����![]() ��
��
��![]() ��
��
�߶��κ���w=![]() �Ķ��������ǣ�60��1200����
�Ķ��������ǣ�60��1200����
�൱x=60 ʱ��w�����ֵ��w���=1200��
��ÿ��ƻ�������ۼ�Ϊ60Ԫʱ�����Ի������������������1200Ԫ��
��3����![]() ����
����![]() ��58��
��58��
��![]() ��58��
��58��
�߶��κ���w=![]() �У�
�У�![]() ���������£��Գ�����ֱ��
���������£��Գ�����ֱ��![]() ��
��
�൱![]() ʱ��w��ֵ��xֵ�����������
ʱ��w��ֵ��xֵ�����������
�൱x=58ʱ��w�����ֵ��w���=1188��
�𣺴�ʱƽ��ÿ���õ����������1188Ԫ��

����Ŀ����֪������![]()
![]() �Գ���Ϊ______����������Ϊ______��
�Գ���Ϊ______����������Ϊ______��
![]() ������ϵ��������㷨�����������ߣ�
������ϵ��������㷨�����������ߣ�
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
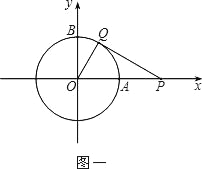
![]() ����������x�ύ��ΪA��B����
����������x�ύ��ΪA��B����![]() ���������ϣ���
���������ϣ���![]() �������
�������