题目内容
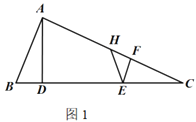
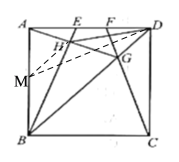
【题目】如图，在边长为4的正方形
中，
是
边上的两个动点，且
，连接
，
与
交于点
，连接
交
于点
，连接
，下列结论：①
；②
平分
；③
；④
；⑤线段的最小值是
．正确的个数有（ ）
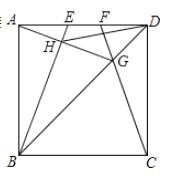
A.2个B.3个C.4个D.5个
【答案】C
【解析】
首先证明
、
、
，然后利用全等三角形的性质、等高模型、三边关系一一判断即可
解：∵四边形ABCD是正方形
∴∠ABD=∠CBD=45°，AB=CB，AD∥BC
又∵BD=BD
∴
∵AD∥BC
∴
∴
故①正确
同理可得：
∴∠DAG=∠DCG
∵
，∠BAE=∠CDF=90°，AB=DC
∴
∴∠ABE=∠DCF
∴∠DAG=∠ABE
∵∠DAG+∠BAG=90°
∴∠ABE+∠BAG=90°
∴
故③正确
∵△HBG、△HDG等高
∴
故④正确
取AB中点M，连接HM、DM
∵正方形
边长为4，△AHB为直角三角形
∴AM=MH=
AB=2
由勾股定理可得DM=
由三角形三边关系得：O、D、H三点共线时，DH最小，最小值=2
-2 故⑤正确
∵E、F为两个动点
∴无法证明DH平分∠EHG，故②错误
故①③④⑤正确，正确结论有4个
故选：C
名校课堂系列答案
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况，从该校九年级136名女生中，随机抽取了20名女生，进行了1分钟仰卧起坐测试，获得数据如下：
收集数据：抽取20名女生的1分钟仰卧起坐测试成绩(个)如下：
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
（1）整理、描述数据：请你按如下分组整理、描述样本数据，把下列表格补充完整：
范围 |
|
|
|
|
|
|
|
人数 |
(说明：每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
（2）分析数据：样本数据的平均数、中位数、满分率如下表所示：
平均数 | 中位数 | 满分率 |
46.8 | 47.5 |
|
得出结论：①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数；
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下：
平均数 | 中位数 | 满分率 |
45.3 | 49 |
|
请你结合该校样本测试成绩和该区县总体测试成绩，为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估．
