ƒøƒ⁄»›
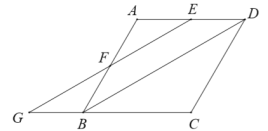
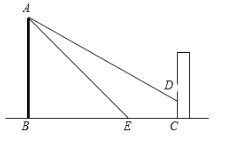
°æƒø°ø»ÁÕº1£¨ƒ≥Õ¨—ߺ“µƒ“ª√Ê¥∞ªß…œ∞≤◊∞”–’⁄—Ù≈Ò£¨Õº2∫ÕÕº3 «Ωÿ√Ê æ“‚Õº£¨CD «’⁄—Ù≈Ò£¨¥∞ªßABŒ™1.5√◊£¨BCŒ™0.5√◊£Æ∏√’⁄—Ù≈Ò”–…ÏÀı𶃋£Æ»ÁÕº2£¨∏√Õ¨—ß‘⁄œƒºæƒ≥»’µƒ’˝ŒÁ ±øÃ≤‚µ√ô—Ùπ‚∫ÕÀÆ∆Ωœflµƒº–Ω«Œ™60°„£¨’⁄—Ù≈ÒCD’˝∫√Ω´Ω¯»Î¥∞ªßABµƒ—Ùπ‚µ≤◊°£ª»ÁÕº3£¨∏√Õ¨—ß‘⁄∂¨ºæƒ≥»’µƒ’˝ŒÁ ±øÃ≤‚µ√ô—Ùπ‚∫ÕÀÆ∆Ωœflµƒº–Ω«Œ™30°„£¨Ω´’⁄—Ù≈Ò ’Àı≥…CD°‰ ±£¨’⁄—Ù≈Ò’˝∫√ÕÍ»´≤ªµ≤Ω¯»Î¥∞ªßABµƒ—Ùπ‚£Æ
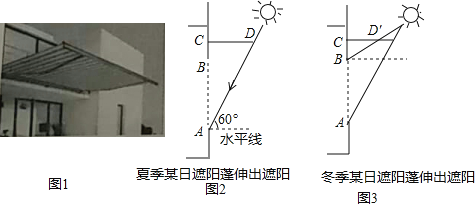
£®1£©º∆À„Õº3÷–CD°‰µƒ≥§∂»±»Õº2÷–CDµƒ≥§∂» ’Àı¡À∂‡…Ÿ√◊£ª£®Ω·π˚±£¡Ù∏˘∫≈£©
£®2£©»Áπ˚Õº3÷–’⁄—Ù≈Òµƒ≥§∂»Œ™Õº2÷–CDµƒ≥§∂»£¨«Îº∆À„∏√’⁄—Ù≈Ò¬‰‘⁄¥∞ªßAB…œµƒ“ı”∞≥§∂»Œ™∂‡…Ÿ√◊£ø£®«Î‘⁄Õº3÷–ª≠Õº≤¢±Í≥ˆœ‡”¶◊÷ƒ∏£¨»ª∫Û‘Ÿº∆À„£©
°æ¥∞∏°ø£®1£©Õº3÷–CD°‰µƒ≥§∂»±»Õº2÷–CDµƒ≥§∂» ’Àı¡À![]() √◊£ª£®2£©∏√’⁄—Ù≈Ò¬‰‘⁄¥∞ªßAB…œµƒ“ı”∞≥§∂»Œ™
√◊£ª£®2£©∏√’⁄—Ù≈Ò¬‰‘⁄¥∞ªßAB…œµƒ“ı”∞≥§∂»Œ™![]() √◊£Æ
√◊£Æ
°æΩ‚Œˆ°ø
£®1£©Ω‚÷±Ω«°˜ACD£¨«Û≥ˆCD£¨‘ŸΩ‚÷±Ω«°˜BCD°‰£¨«Û≥ˆCD°‰£¨»ª∫Ûº∆À„CD©ÅCD°‰µƒ≥§∂»º¥ø…£ª
£®2£©Õº3÷–’⁄—Ù≈Óµƒ≥§∂»Œ™Õº2÷–CDµƒ≥§∂» ±£¨π˝D◊˜DE°ŒBD°‰£¨ΩªAB”⁄E£¨Ω‚÷±Ω«°˜ECD£¨«Û≥ˆCE£¨‘Ÿº∆À„CE-BCº¥ø…£Æ
£®1£©‘⁄÷±Ω«°˜ACD÷–£¨°flAC£ΩAB+BC£Ω2√◊£¨°œCAD£Ω30°„£¨
°‡tan°œCAD£Ω![]() £¨
£¨
°‡CD£ΩACtan°œCAD£Ω2°¡![]() £Ω
£Ω![]() £®√◊£©£Æ
£®√◊£©£Æ
‘⁄÷±Ω«°˜BCD°‰÷–£¨°flBC£Ω0.5√◊£¨°œCBD°‰£Ω60°„£¨
°‡tan°œCBD°‰£Ω![]() £¨
£¨
°‡CD°‰£ΩBCtan°œCBD°‰£Ω0.5°¡![]() £Ω
£Ω![]() £®√◊£©£¨
£®√◊£©£¨
°‡CD©ÅCD°‰£Ω![]() ©Å
©Å![]() £Ω
£Ω![]() £®√◊£©£Æ
£®√◊£©£Æ
π Õº3÷–CD°‰µƒ≥§∂»±»Õº2÷–CDµƒ≥§∂» ’Àı¡À![]() √◊£ª
√◊£ª
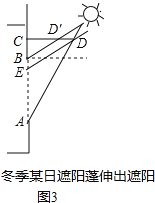
£®2£©»ÁÕº£¨Õº3÷–’⁄—Ù≈Òµƒ≥§∂»Œ™Õº2÷–CDµƒ≥§∂» ±£¨π˝D◊˜DE°ŒBD°‰£¨ΩªAB”⁄E£Æ
‘⁄÷±Ω«°˜ECD÷–£¨°flCD£Ω![]() √◊£¨°œCED£Ω60°„£¨
√◊£¨°œCED£Ω60°„£¨
°‡tan°œCED£Ω![]() £¨
£¨
°‡CE£Ω![]() £Ω
£Ω![]() £Ω
£Ω![]() £¨
£¨
°‡BE£ΩCE©ÅBC£Ω![]() ©Å0.5£Ω
©Å0.5£Ω![]() £®√◊£©£Æ
£®√◊£©£Æ
π ∏√’⁄—Ù≈Ò¬‰‘⁄¥∞ªßAB…œµƒ“ı”∞≥§∂»Œ™![]() √◊£Æ
√◊£Æ

 ◊€∫œ◊‘≤‚œµ¡–¥∞∏
◊€∫œ◊‘≤‚œµ¡–¥∞∏