题目内容
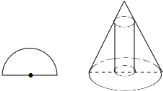
【题目】将半径为![]() 的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________
的半圆围成一个圆锥,在圆锥内接一圆柱(如图)当圆柱的侧面的面积最大时,圆柱的底面半径是________![]() .
.
【答案】2
【解析】
根据弧长公式可求出扇形的弧长,进而可得到圆锥的底面半径,利用勾股定理即可求得圆锥的高,利用相似可求得圆柱的高与母线的关系,表示出侧面积,根据二次函数求出相应的最值时自变量的取值即可
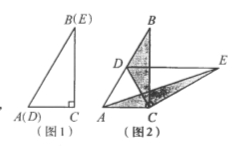
如图:扇形的弧长=8πcm,
∴圆锥的底面半径=8π÷2π=4cm,
∴圆锥的高为![]() =4
=4![]() cm,
cm,
设圆柱的底面半径为r,高为h.则BC=r,AD=h,
∵BC//DE,
∴△ABC∽△ADE,
∴![]()
解得:h=![]() (4-r),
(4-r),
∴圆柱的侧面积=2π×r×![]() (4-r)=-2
(4-r)=-2![]()
![]() (r-2)2+8
(r-2)2+8![]() π,
π,
∴r=2时,圆柱的侧面积有最大值,

故答案为:2

练习册系列答案
相关题目