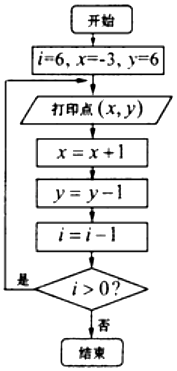
��Ŀ����
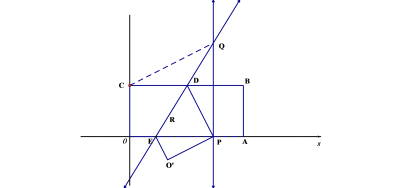
����Ŀ����ͼ1��ʾ,������OABC����ƽ��ֱ������ϵ��,��A,C�ֱ���x,y�����������,��֪��B(4,2),������OABC����,ʹ�õ�C�Ķ�Ӧ��Pǡ�������߶�OA(�����˵�O,A)��,�ۺ�����ֱ�߷ֱ�BC��OA�ڵ�D��E������P���߶�OA���˶�ʱ,����P��OA�Ĵ��߽��ۺ�����ֱ���ڵ�Q. 
��1����֤��CQ=QP
��2�����Q������Ϊ(x,y),��y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ;
��3����ͼ2,����OQ,OB,����P���߶�OA���˶�ʱ,��������OBQ�����ΪS,��xȡ��ֵʱ,Sȡ����Сֵ,�������Сֵ��
���𰸡�
��1��
�⣺����CQ��
����֪��CD=PD,
��CDE=��PDE,
�� ��CDQ=��PDQ,
��DQ=DQ,
���CDQ�ա�PDQ��CQ=PQ.
��2��
�⣺��Q(x,y) �� CQ=PQ=y
��BC��PQ�Ľ���ΪM����QM=y-2,CG=x
�ɹ��ɶ�������
x2+(y-2)2=y2��
��y=![]() +1(0<x<4).
+1(0<x<4).
��3��
�⣺��ֱ��OB��ֱ��PQ�ཻ�ڵ�G(x��y')��
��ΪB��4,2��������ֱ��OBΪy=![]() ��
��
��Ϊ��G��ֱ��OB�ϣ���y'=![]() ��
��
��QG=![]() x2+1-
x2+1-![]() x
x
��S=![]() ��4��
��4��![]() x2-
x2-![]() x+1��=
x+1��=![]() x2-x+2��
x2-x+2��
��x=1ʱ��S����СֵΪ![]() .
.

����������1������CQ�����۵���������CD=PD,����CDE=��PDE,���CDQ=��PDQ����DQ=DQ,�ɵá�CDQ�ա�PDQ��CQ=PQ��
��2��CQ=PQ=y����ֱ��������CQM�У�QM2+CM2=CQ2 �� �ɽ��y��x�Ĺ�ϵ��
��3����G���Q�ĺ�������ͬ���ɵ�G��OB���õ�G�������꣬��֪QG�ij�����S=S��OQG+S��BQG �� �ɵõ�S��x�Ĺ�ϵʽ��������ֵ.
�����㾫�������ڱ��⿼��Ķ��κ��������ʺͶ��κ�������ֵ����Ҫ�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a���ܵó���ȷ�𰸣�

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�����Ŀ��ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]�� 
��1����ͼ��a��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����ijɼ���ƽ���֣�
��3������100��ѧ�����ijɼ�ijЩ�����ε�������x������ѧ�ɼ���Ӧ�����ε�������y��֮�������ʾ������ѧ�ɼ���[50��90��֮���������
������ | [50��60�� | [60��70�� | [70��80�� | [80��90�� |
x��y | 1��1 | 2��1 | 3��4 | 4��5 |