Question

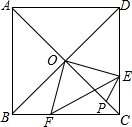
将正方形的四个顶点用线段连接起来，怎样的连线最短？研究发现，并非连对角线最短，而是如图的连线更短（即用线段AE、BE、EF、CF、DF把四个顶点连接起来）．已知图中ABCD是正方形，∠BAE=∠ABE=∠FDC=∠FCD=30°，∠AEF=∠DFE且AE=DF．
（1）请你证明AD∥EF；
（2）设正方形边长为2，计算连线AE+BE+EF+CF+DF的长度．

Answer 1

延长EF与CD交于点G，延长FE与AB交于H点，
∵∠AEF=∠DFE，∴∠AEH=∠DFG，
∵∠EAH=∠FDG，AE=DF
∴△AEH≌△DFG，
∴AH=DG，

（1）∵∠AEF=∠DFE，∠BAE=∠FDC=30°
∴∠EAD=∠FDA，且AE=DF
∴四边形ADFE是等腰梯形，且EF∥AD，

（2）正方形ABCD的边长为2，
则在直角△AEH中，AH=BH=1，
∴AE=

AH

cos30°

=

1

3 2

=

2

3

=

2 3

3

，
EH=

3

3

，
即EF=2-

2 3

3

，
故AE+BE+EF+CF+DF，
=4×

2 3

3

+2-

2 3

3

，
=2+2

3

．
答：AE+BE+EF+CF+DF的长度为2+2

3

．