题目内容
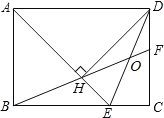
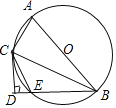
【题目】如图,已知AB是⊙O的直径,BE是⊙O的弦,BC是∠ABE的平分线且交⊙O于点C,连接AC,CE,过点C作CD⊥BE,交BE的延长线于点D.
(1)∠DCE ∠CBE;(填“>”“<”或“=”)
(2)求证:DC是⊙O的切线;
(3)若⊙O的直径为10,sin∠BAC=![]() ,求BE的长.
,求BE的长.
【答案】(1)=;(2)见解析;(3)2.8.
【解析】
(1)由AB为⊙O的直径,得到∠ACB=90°,求得∠ACB=∠D,根据角平分线的性质得到∠ABC=∠CBD,通过相似三角形得到∠BAC=∠BCD,四边形ABEC是圆内接四边形,得出∠CED=∠BAC,根据余角的性质即可证得∠DCE=∠CBE;
(2)连接OC,由等腰三角形的性质得出∠OBC=∠OCB,等量代换得到∠OCB=∠CBD,证得OC∥BD,即可证得OC⊥CD,即可得到结论;
(3)解直角三角形ABC求得BC,进而求得AC,通过三角形相似的性质得出CD=4.8,BD=6.4,进而求得DE=3.6,即可求得BE=2.8.
(1)解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD⊥BE
∠D=90°,
∴∠ACB=∠D,
∵BC是∠ABE的平分线,
∴∠ABC=∠CBD,
∴△ABC∽△CBD,
∴∠BAC=∠BCD,
∵四边形ABEC是圆内接四边形
∴∠CED=∠BAC,
∵∠DBC+∠BCD=90°,∠ECD+∠CED=90°
∴∠DCE=∠CBE;
故答案为:=;
(2)证明:连接OC,
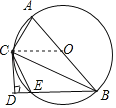
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=∠CBD
∴∠OCB=∠CBD,
∴OC∥BD,
∵CD⊥BD,
∴OC⊥CD,
∴CD是⊙O的切线;
(3)解:∵⊙O的直径为10,sin∠BAC=![]() ,
,
∴sin∠BAC=![]() =
=![]() ,
,
∴BC=8,
∴AC=![]() =6,
=6,
∵△ABC∽△CBD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴CD=4.8,BD=6.4,
∵∠CDE=∠ACB=90°,∠CED=∠BAC,
∴△CED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DE=3.6,
∴BE=BD﹣DE=6.4﹣3.6=2.8.