题目内容
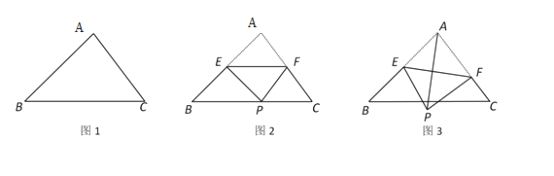
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
【答案】(1)4;(2)①90°;②![]()
【解析】
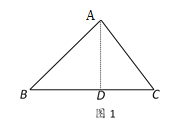
(1)如图1中,过点A作AD⊥BC于D.解直角三角形求出AD即可.
(2)①证明BE=EP,可得∠EPB=∠B=45°解决问题.
②如图3中,由(1)可知:AC=![]() ,证明△AEF∽△ACB,推出
,证明△AEF∽△ACB,推出![]() ,由此求出AF即可解决问题.
,由此求出AF即可解决问题.
解:(1)如图1,过点A作AD⊥BC于点D,
在Rt△ABD中,![]() =
=![]() =4.
=4.
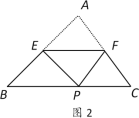
(2)①如图2,∵△AEF≌△PEF,
∴AE=EP.
又∵AE=BE ,
∴BE=EP,
∴∠EPB=∠B=45°,
∴∠AEP=90°.
②如图3,由(1)可知:在Rt△ADC中,![]() .
.
∵PF⊥AC,
∴∠PFA=90°.
∵△AEF≌△PEF,
∴∠AFE=∠PFE=45°,则∠AFE=∠B.
又∵∠EAF=∠CAB,
∴△EAF∽△CAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AF=![]() ,
,
在Rt△AFP中,AF=PF,则AP=![]() =
=![]() .
.

练习册系列答案
相关题目